Trigonal and Hexagonal Space Group Symbols 2
The image on the left is the space group diagram of \(P312\), while the image on the right is \(P321\). The best way to check is look for whether a two-fold rotation axis parallel to \(a\) (or \(b\), remembering that these are equivalent axes in trigonal lattices) is present. If the two-fold rotation is parallel to a unit cell vector, the symbol \(2\) is in the second position of the space group symbol.

One of the below images is \(P6_{3}mc\) while the other is \(P6_{3}cm\). Which is which? The answer is at the bottom of the page!
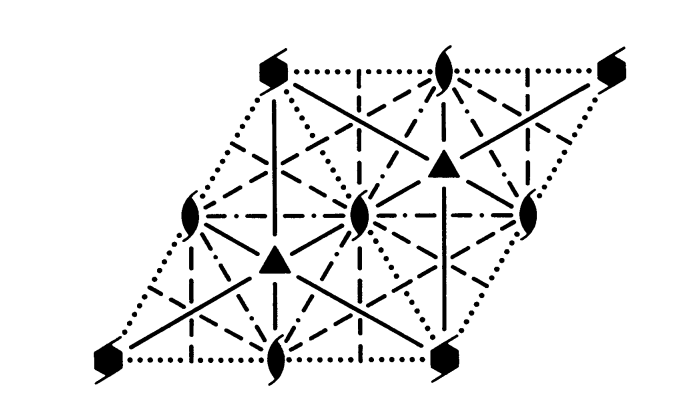
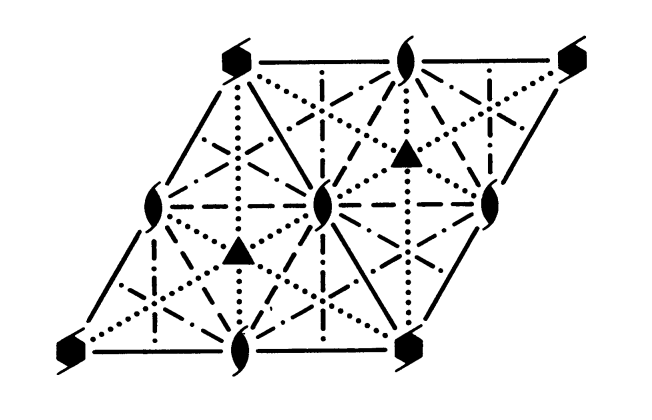
The diagram on the left is \(P6_{3}mc\) as there is a mirror plane present perpendicular to \(a\) (also one perpendicular to \(b\), as these axes are equivalent!). The diagram on the right is \(P6_{3}cm\) as the \(c\) glide is perpendicular to \(a\), while the mirror plane is perpendicular to \(\mathbf{a}-\mathbf{b}\).