Trigonal and Hexagonal Space Group Symbols
Despite the different settings possible for trigonal space groups, the vectors used to define their space group symbols are identical in each setting. Consider the space group \(R3c\) shown below.
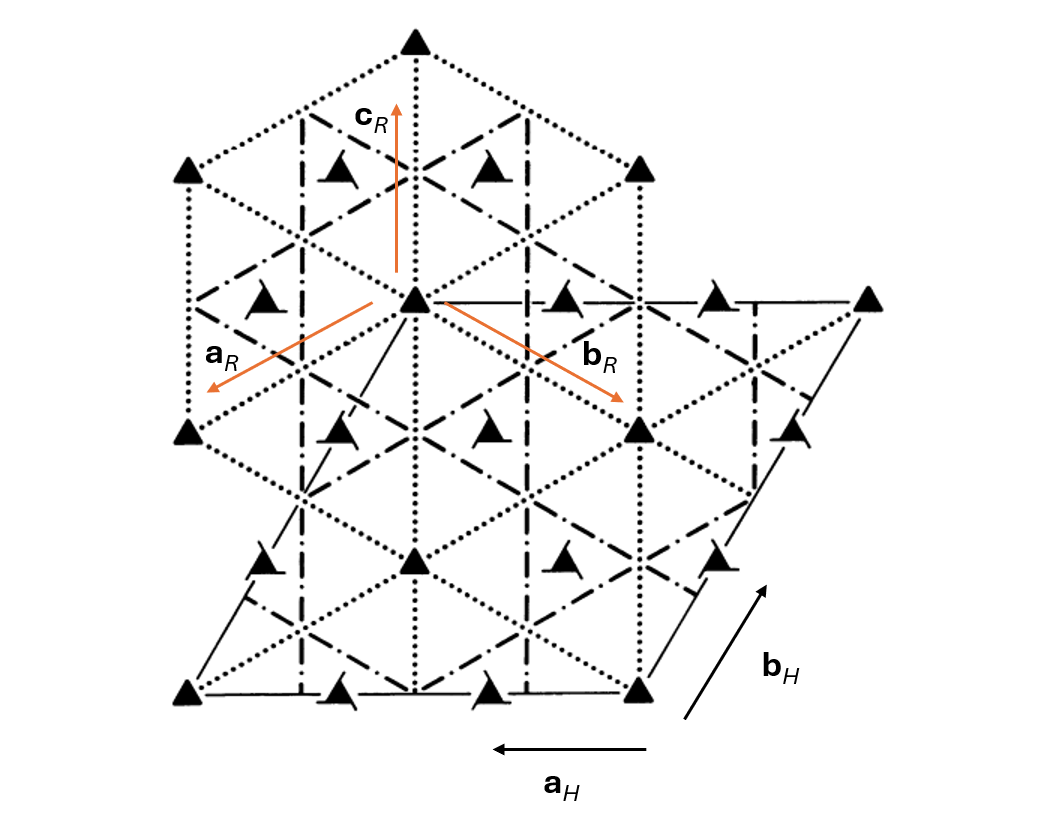
Both hexagonal and rhombohedral unit cells are shown. It should be noted that 2D representations of rhombohedral unit cells do not typically show the 3D nature of the cell well. Nonetheless, the vector \(\mathbf{c}_{H}\) is parallel to the vector \(\mathbf{a}_{R} + \mathbf{b}_{R} + \mathbf{c}_{R}\). Similarly, the vector \(\mathbf{a}_{R}-\mathbf{b}_{R}\) is parallel to the vector \(\mathbf{a}_{H}\).
The space group symbol \(R3c\) implies rhombohedral lattice point centring, a three-fold rotation axis parallel to \(\mathbf{c}_{H}\) and a \(c_{H}\) glide plane perpendicular to \(\mathbf{a}_{H}\). These can be seen in the diagram above. The combination of these symmetry elements produces the other symmetry elements present in the diagram.
For hexagonal or non-rhombohedral trigonal lattices, a third symbol might be given, corresponding to the unique axis \(\mathbf{a}_{H}-\mathbf{b}_{H}\). It would be a good exercise to determine the direction of the vector on the diagram above. It is crucially different to the vector \(\mathbf{a}_{H}+\mathbf{b}_{H}\)
Consider the two space group diagrams below. Which is \(P312\) and which is \(P321\)? Consider the unique axes of the two-fold rotations to help you. The answers are on the next page.