Cubic Space Group Symbols
Cubic space group diagrams can be confusing because of the large number of symmetry elements usually present in these space groups. Their symbols are formed from the unique axes \(\mathbf{c}\), \(\mathbf{a} + \mathbf{b} + \mathbf{c}\) and \(\mathbf{a} – \mathbf{b}\). Remembering that \(\mathbf{a}\), \(\mathbf{b}\) and \(\mathbf{c}\) are equivalent and interchangeable in cubic symmetry, these unique axis vectors are equivalent to the unique axes of an edge, a body diagonal of the cube, and a diagonal of the face of the cube.
Where only two symbols are given, these correspond to the first two positions of the space group symbol.
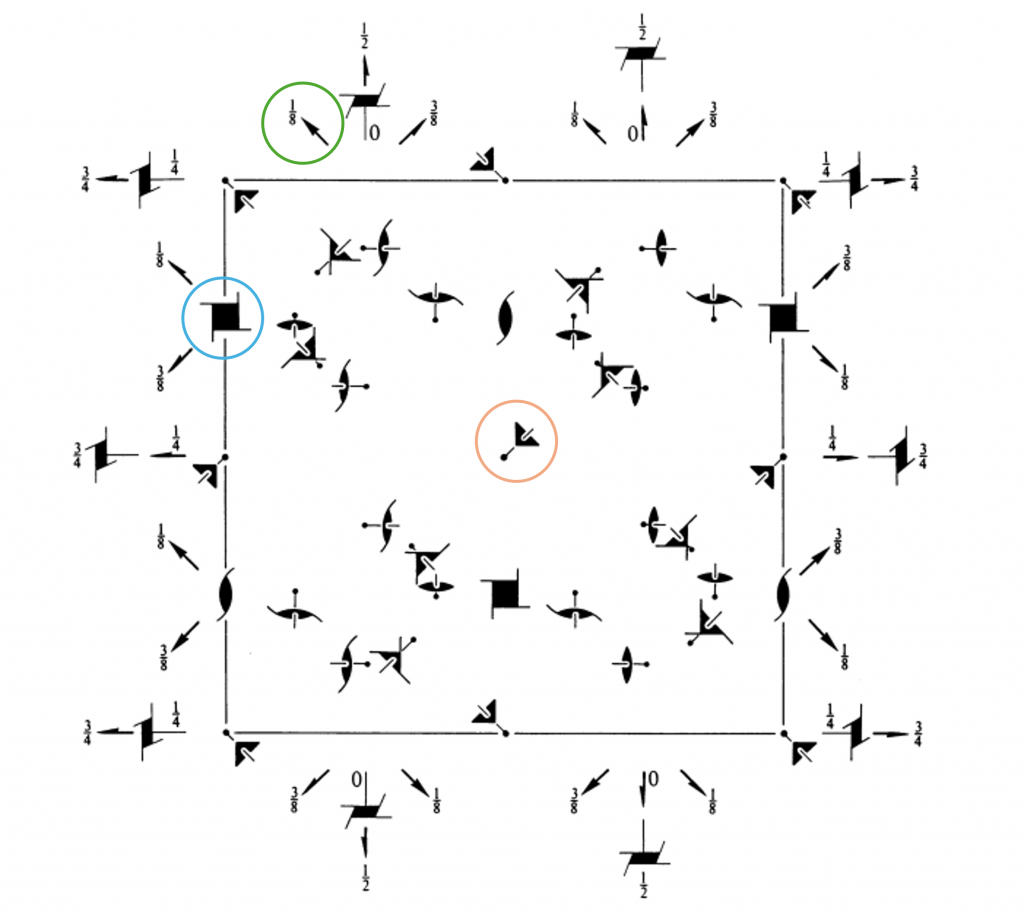
Above is the space group diagram of \(P4_{1}32\). The highlighted symmetry elements correspond to those in the space group symbol. In the blue circle is the \(4_{1}\) screw axis parallel to \(c\). This is also present parallel to \(a\) and \(b\), as it must be in cubic symmetry. In orange is the three-fold rotation axis parallel to \(\mathbf{a} + \mathbf{b} + \mathbf{c}\). This symbol uses a pierced triangle to show the orientation of the three-fold axis is diagonally out of the page, along the diagonal of the cube. In the green circle is the two-fold rotation axis parallel to \(\mathbf{a} – \mathbf{b}\) (the diagonal of the face). Remember, it does not have to be along the face diagonal, merely parallel to it. We could easily move the origin such that it is along the face diagonal if we wished. The symbol of \(\frac{1}{8}\) refers to the height of this rotation axis.