Wyckoff Positions
In the standard unit cell of any space group, an infinite number of locations, defined by the coordinates are possible. However, not all of these are equal. For example, consider the space group diagram of \(P222\) below. If an atom is placed at a ‘general’ position, for example \((0.15, 0.25, 0.35)\), the symmetry of the unit cell mandates there must also be atoms present at \((0.85, 0.75, 0.35)\), \((0.85, 0.25, 0.65)\) and \((0.15, 0.75, 0.65)\). This can be worked out using the effects of two-fold rotation on a position \((x, y, z)\).
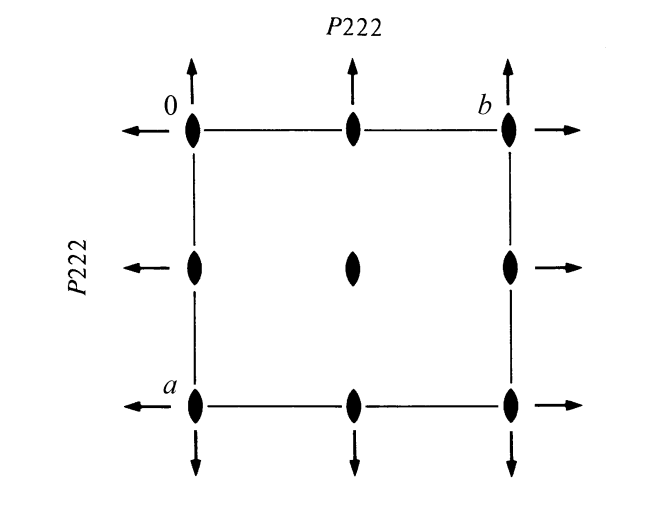
If an atom is placed at a ‘special’ position, a smaller number of atoms is produced by the symmetry. For example, if an atom is placed on a two-fold rotation axis such as the position \((0.5, 0.5, 0.2)\), then applying the two-fold rotation axes parallel to \(c\) has no effect. The only other symmetry-equivalent atom in the unit cell is thus at \((0.5, 0.5, 0.8)\).
If an atom is placed on the point of intersection between all three two-fold rotation axes, \((0.5, 0.5, 0.5)\), all two-fold rotation axes have no effect. As such, no other atom is produced by the symmetry elements. This concept is the origin of Wyckoff positions. Each Wyckoff position in a unit cell is assigned a multiplicity, the number of atoms present in this position, and a Wyckoff letter. The Wyckoff letter is simply an identifier to distinguish between different positions with equivalent multiplicity. Wyckoff letters are assigned from a to z starting with the position with the lowest multiplicity. Also stated in the International Tables are the symmetry elements the Wyckoff position is associated with.
A more complete example is given on the next page.