Glide Planes
Glide planes consist of a reflection in a mirror plane followed by a translation vector.
There are many different translation vectors that are possible, and thus many different symbols representing these. When the glide plane is perpendicular to the viewing axis, a symbol from the left image below is used. When the glide plane is parallel to the viewing axis, a symbol from the right image below is used. It is worth considering what a plane looks like in 3D from different angles. Maybe find a cuboidal item in your kitchen (such as a box of some kind) and imagine what a piece of paper (a plane) through the box looks like from different directions. This will help greatly to understand the origins of the symbols and what it means for a plane to be perpendicular or parallel to the viewing axis.
It would be wise to go through this page slowly. There is a lot to take in.
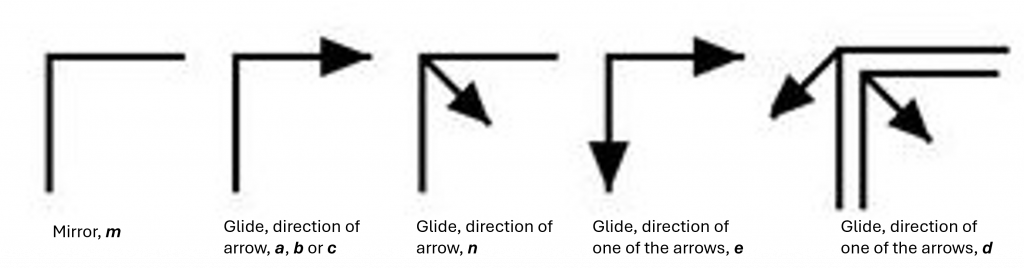
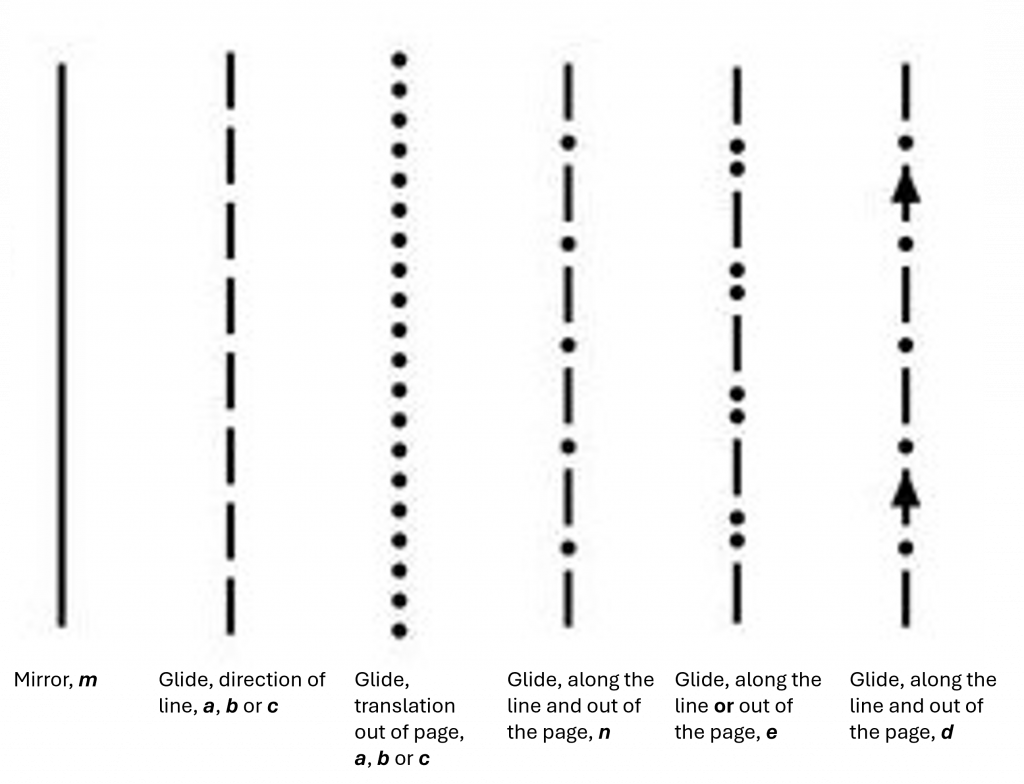
The letter symbols are used to inform about the translation vector. \(a\), \(b\) or \(c\) glides correspond to translation in the direction of the symbol by \(\frac{1}{2}\). An \(n\) glide translates along both lattice vectors possible within the glide plane. This will become clearer with diagrams and as you learn how to use coordinate representations. Below is the space group diagram for \(Pban\) viewed down the \(b\) axis.

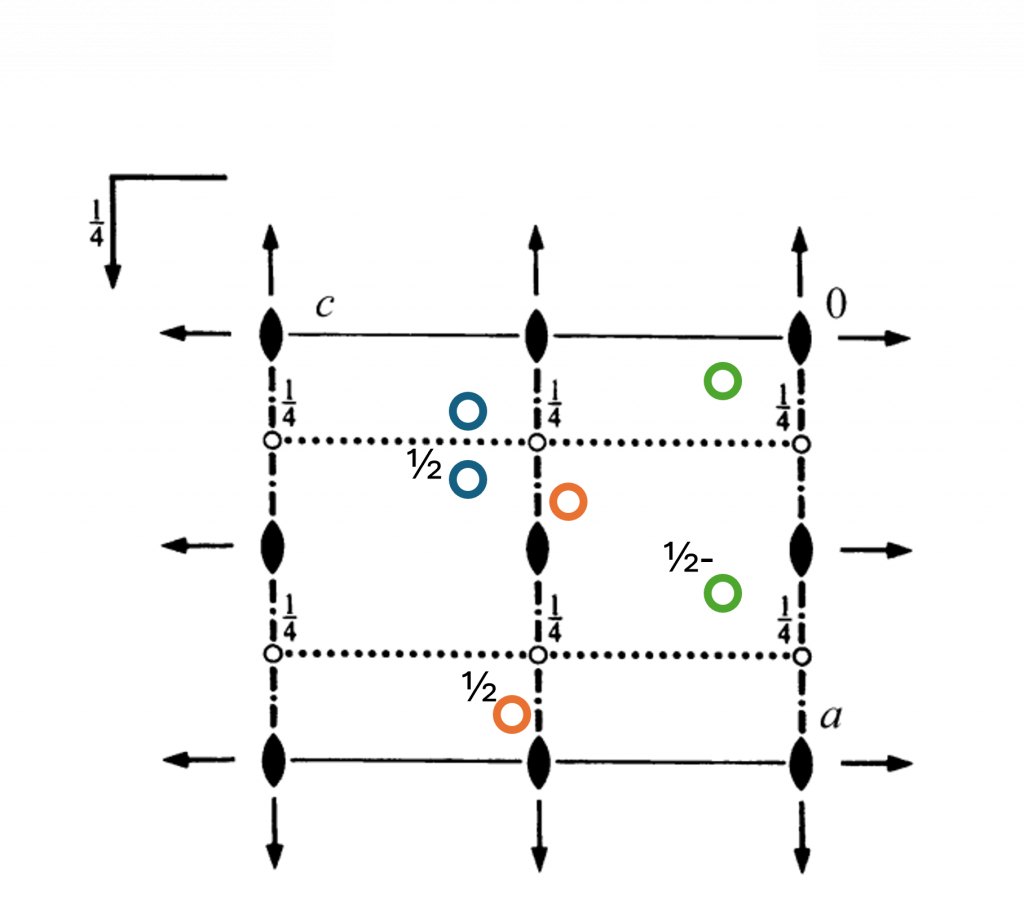
Using the symbols above, identify the \(n\) glide. This \(n\) glide has been enacted on the orange point. First it is reflected through the plane shown, then it is translated a half along the \(a\) axis and a half along the \(b\) axis, the viewing axis. One way to know the translation vectors of an \(n\) glide is by excluding the axis perpendicular to the plane. In the case above, the \(n\) glide is perpendicular to the \(c\) axis, so the translation vectors are \(a\) and \(b\).
Identify the glide plane which is parallel to the viewing axis and has a translation vector out of the page (also parallel to the viewing axis!). In the 2D representation, the \(a\) axis points down (find the origin (0) and the symbol \(a\) on the diagram to identify this). As this glide plane appears horizontal, it is perpendicular to the \(a\) axis. The glide vector is out of the page. In other words, this is along the viewing axis, which is \(b\). Therefore, this glide plane is a \(b\) glide perpendicular to the $a$ axis. This has been enacted on the blue atom. It is first reflected through the plane, then translated out of the page (along the \(b\) axis) by vector of \(\frac{1}{2}\).
The symbol for a glide plane which is perpendicular to the viewing axis and has one translation vector perpendicular to the viewing axis is shown above on the left. It is not hard to determine which direction the translation is in (it’s the direction of the arrow!). In the image above, the green points show the effect of the \(a\) glide plane. This is the glide plane perpendicular to \(b\), the viewing axis, and denoted in the top left of the diagram!
The key points here are that the translation vector is represented by the letter assigned to the plane and this is represented differently on a diagram depending on which axis is the viewing axis in a 2D representation. \(n\) refers to a glide plane with both possible translation vectors applied. \(a\), \(b\) and \(c\) refer to a glide plane with only translation vector applied. The translation vector is made clear by the letter or graphical symbol. The orientation of the plane itself can be determined by which axis it is perpendicular to.
An \(e\) glide refers to either of the translation vectors applying, but not both. This is equivalent to having both an \(a\) and a \(b\) glide plane present in the same position.
A \(d\) glide plane is the same as an \(n\) glide plane but the translation vectors are only \(\frac{1}{4}\) rather than \(\frac{1}{2}\).
This will become much clearer upon working with coordinate representations! I would recommend you have a recap of this page slowly before continuing. It will become clearer in time.