Screw Axes
Screw axes consist of a rotation around the axis followed by a translation in the direction of the axis. The symbol assigned is \(n_{t}\) where \(\frac{360}{n}\) is the angle of rotation and \(\frac{t}{n}\) is the translation vector in fractional coordinates. For \(2_{1}\) screw axes, a \(180^{\circ}\) rotation followed by translation of \(\frac{1}{2}\), the direction of rotation and translation does not matter. This is because a translation by \(+\frac{1}{2}\) and \(-\frac{1}{2}\) are identical in an infinitely repeated lattice. The same applies for the two-fold rotation; an anticlockwise rotation is identical to a clockwise rotation.
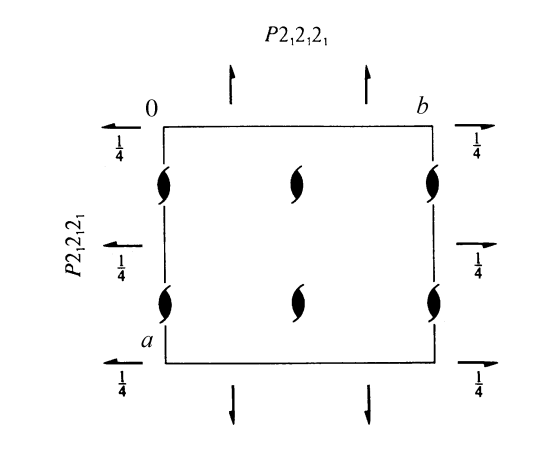
Above is the space group diagram of \(P2_{1}2_{1}2_{1}\). The \(2_{1}\) screw axes parallel to the viewing axis are shown as two-fold rotations with extended edges. The \(2_{1}\) screw axes perpendicular to the viewing axis are shown as hooks. The height of these axes is shown when the height is not 0.
Below is the space group diagrams of \(P3_{1}\) and \(P3_{2}\). Note the different direction on the extended edges of the triangular symbols used to represent the screw axes. Now the rotation is no longer two-fold, the relative direction of rotation and translation does matter. In order to perform these operations correctly, do the rotation ‘anticlockwise’ and the translation ‘up’ (i.e. out of the page towards the viewer). Of course these definitions depend on which direction you look down the axis. If the viewing direction is kept consistent for both rotation and translation then this method will work. As mentioned, it is only the relative direction of rotation and translation that matter, so rotating ‘clockwise’ and translating ‘down’ is also acceptable. Never rotate clockwise and translate up, or rotate anticlockwise and translate down.
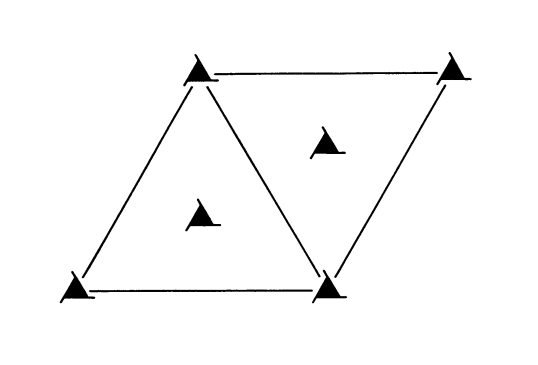
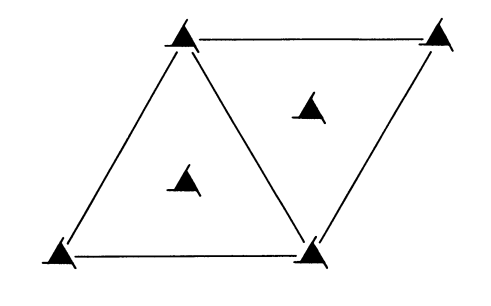
It may sound like applying the \(3_{2}\) screw axis to a point multiple times may lead to it ending up two unit cells above. After all, the translation vector is \(\frac{2}{3}\). Applying this translation three times gives a translation vector of \(2\mathbf{c}\). However, due to the periodicity of the lattice, the point \((x, y, z+2\mathbf{c})\) is identical to the point \((x, y, z)\).
Four-fold and six-fold screw axes also exist and should be treated with caution the same way as three-fold screw axes.