Roto-Inversion
Roto-inversion refers to a rotation followed by an inversion. An axis is defined for the rotation, however a point must be defined for the inversion process. This point is always on the rotation axis. Only three roto-inversions are unique. It is relatively simple to show that a two-fold and three-fold roto-inversion are the same as other symmetry elements, though this is a good exercise for the reader. This will be covered in the section working on coordinate representations.
Only the one-fold (inversion centre) and four-fold roto-inversions are truly new symmetry elements, though understanding the process leads to understanding them all. A one-fold roto-inversion is more commonly known as an inversion centre, and simply leads to inversion through a point. The inversion centre is simply represented as an unfilled circle. The four-fold roto-inversion is represented as the symbol for a two-fold rotation inside an unfilled square. These do not come up as often as other symmetry elements but must be understood nonetheless.
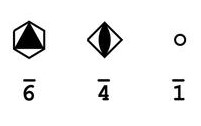
The six-fold roto-inversion is used in the space group \(P\bar{6}\), though it can be considered the combination of a three-fold rotation and a mirror plane perpendicular to the three-fold rotation.