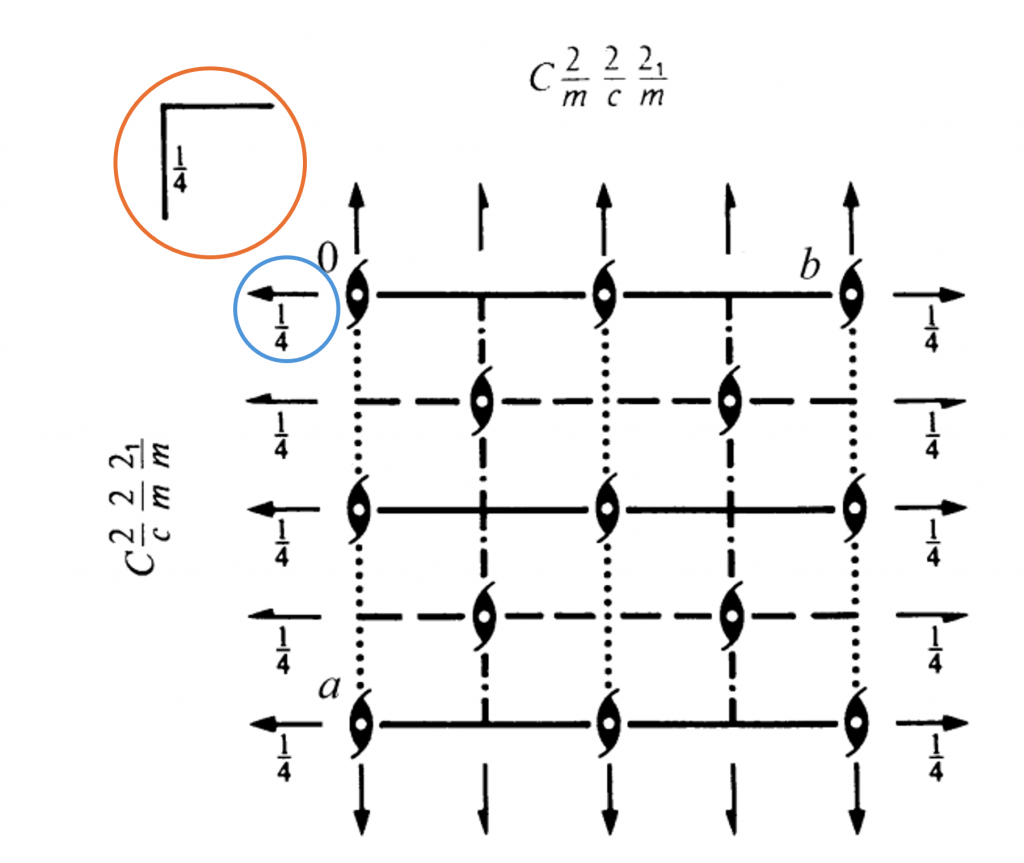
Mirror Planes
Mirror planes are represented as bold lines in space group diagrams when parallel to the viewing axis. They are represented as a right angle in the top corner of the diagram when perpendicular to the viewing axis. Below is the space group diagram of \(Pmmm\). Note the mirror planes shown as bold lines at \((0+\frac{n}{2}, b, c)\) and \((a, 0+\frac{n}{2}, c)\). In the top left hand corner is the symbol for a mirror plane present perpendicular to the viewing axis (the \(c\) axis).
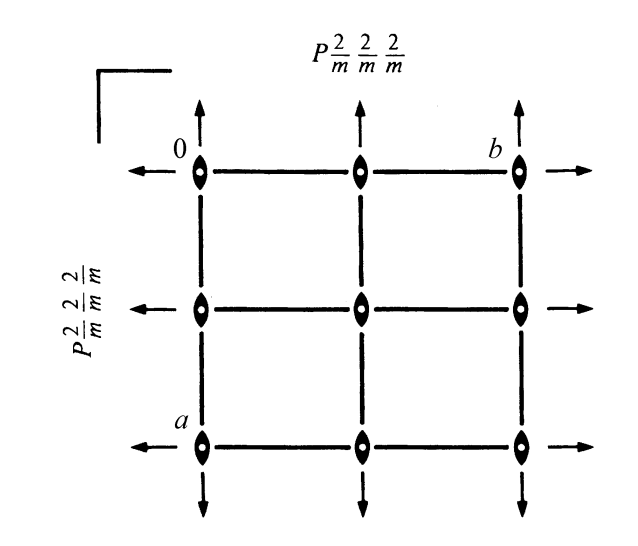
The symbol for a mirror plane or a rotation axis perpendicular to the viewing axis can sometimes have a fraction next to it. This represents the height of the symmetry element. This can be seen below in the space group diagram of \(Cmcm\). The symbol for a mirror plane has a \(\frac{1}{4}\) next to it. This signifies the mirror planes are at a height of \(\frac{1}{4}\) and \(\frac{3}{4}\), rather than the usual \(0\) and \(\frac{1}{2}\). The same can be seen for the two-fold rotation axis highlighted in the blue circle. Space group diagrams for high-symmetry space groups can get complicated quickly.