Rotation Axes
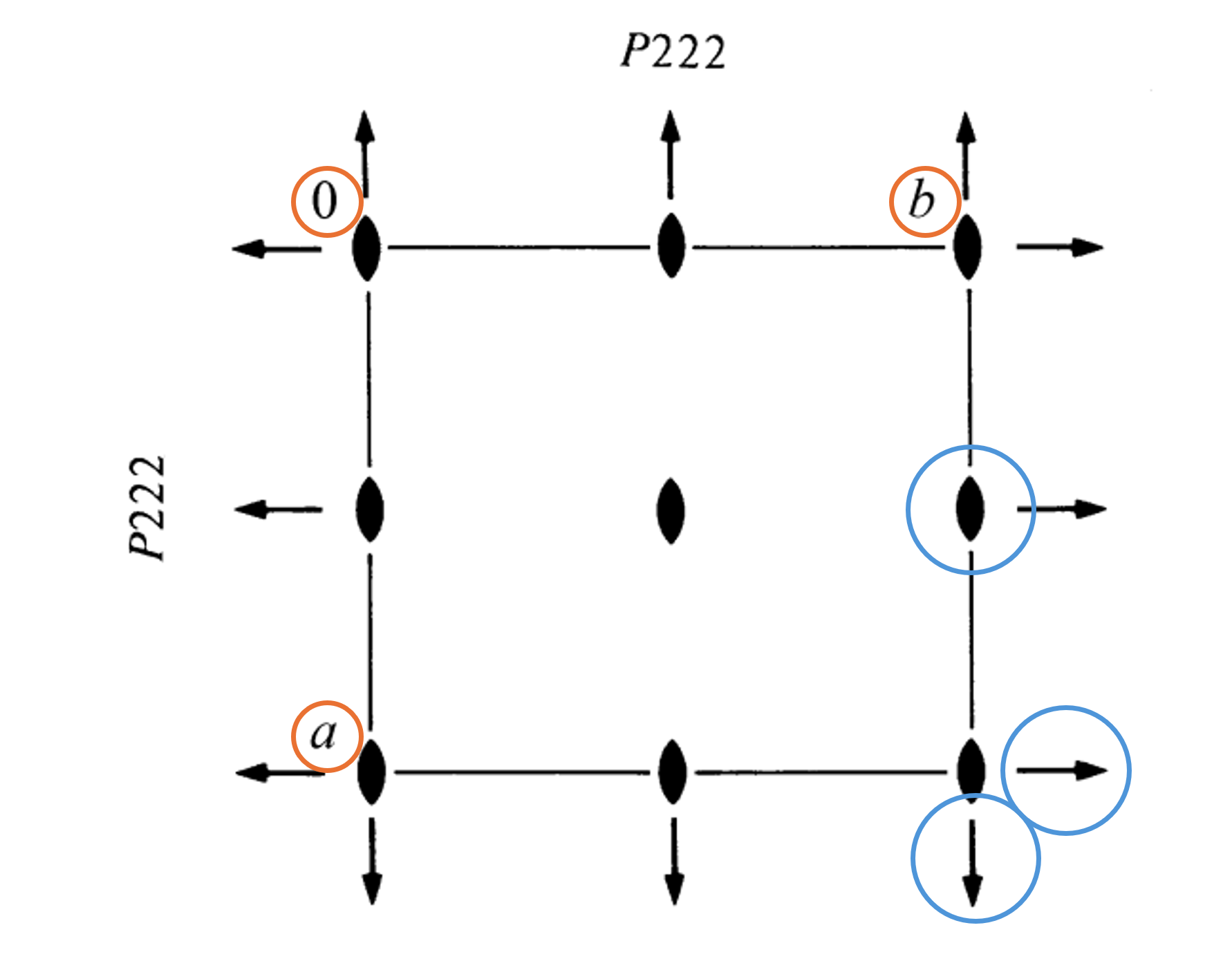
Consider the space group diagram for the space group \(P222\) below. This image is taken from The International Tables for Crystallography. This space group has three two-fold rotation axes along each of its orthorhombic axes. The symbols \(0\), \(a\) and \(b\), highlighted in orange, refer to the origin, the \(a\) and the \(b\) axes respectively. This means the \(a\) vector points from the origin to the the \(a\) symbol in the current representation. This means we are looking down the \(c\) axis in this form. The International Tables will often give multiple representations of the space group diagram. Highlighted in blue are the two-fold rotation axes. The concave lens symbol shows a two-fold rotation axis parallel to \(c\). These are repeated due to the nature of the translational symmetry and are located at \((0 + \frac{n}{2}, 0 + \frac{n}{2}, c)\).
Below are the space group diagrams for \(P4\), \(P3\) and \(P6\) (left to right). Note the symbols for how different rotation axes are represented.
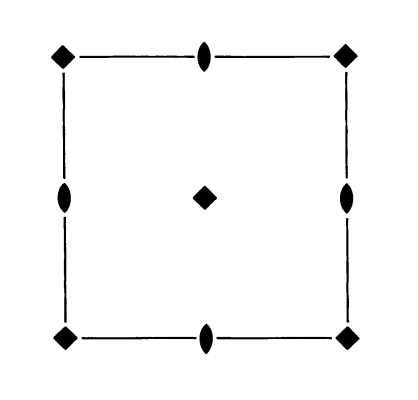
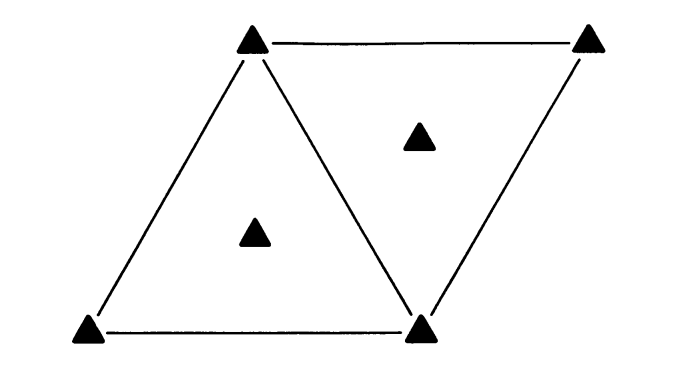
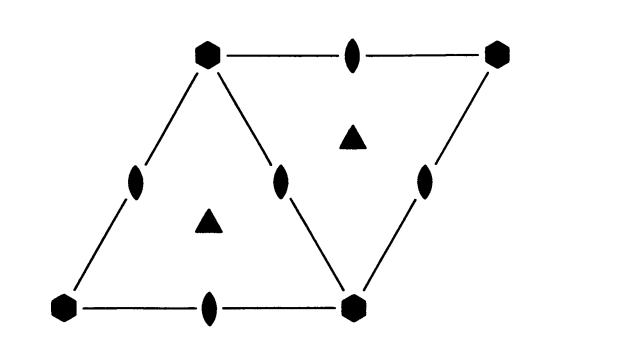
Four-fold, three-fold and six-fold axes are often the principle rotation axes and so it would be rare to need or attempt to represent them in any other direction. Four-fold rotation axes can appear perpendicular to the viewing axis in cubic space groups. These are shown as a square at the end of a line. Three-fold axes can also appear diagonally in cubic space groups. These are shown as triangles with lines through the middle.