Representations of Symmetry Elements
Symmetry elements you will need to know and understand are the following:
- Rotation Axes
- Mirror Planes
- Screw Axes
- Glide Planes
- Roto-Inversion Axes
On a space group diagram, symmetry elements often need representation parallel and perpendicular to the viewing axis/plane of the page. As such, many have two symbols to represent them depending on the direction in which they operate.
Rotation axes, unsurprisingly consist of rotation around an axis. They are simply given a number to represent their \(\frac{360^{\circ}}{n}\) rotation i.e. a 2 refers to a two-fold rotation axis which is a \(180^{\circ}\) rotation. They are shown on a diagram using a symbol that possesses the relevant rotation symmetry (triangle for three-fold, square for four-fold).
Mirror planes are simply shown on a diagram using bold lines and are given the symbol \(m\). Be careful not to confuse these with the boundaries of the unit cell, though the boundaries of the unit cell may overlap with mirror planes.
Screw axes consist of a rotation followed by a translation along the direction of the axis. This is a key difference to point group determination. Point groups do not deal with translational symmetry, while this is an added layer of complexity for space groups. These are given symbols with extended edges to represent the translation. They are given symbols such as \(n_{t}\). \(n\) refers to the rotation element, while \(\frac{t}{n}\) is the translation required in fractional coordinates. Hence, a \(3_{1}\) screw axis is a \(120^{\circ}\) rotation followed by a translation of \(\frac{1}{3}\) along the direction of the axis.
Glide planes are mirror planes followed by a translation element. Enacting the glide plane involves reflection followed by translation. Various symbols are given to these depending on the translation vector required. They are typically represented graphically as dashed or dotted lines.
Roto-inversion axes refer to a rotation around an axis followed by an inversion through a point on this axis. The point is specified. It is not an inversion through the closest point on the axis. These are represented graphically using the symbol for an \(\frac{n}{2}\) rotation inside the symbol for an \(n\)-fold rotation.
These symbols are below. They will be discussed in more detail in the coming pages.
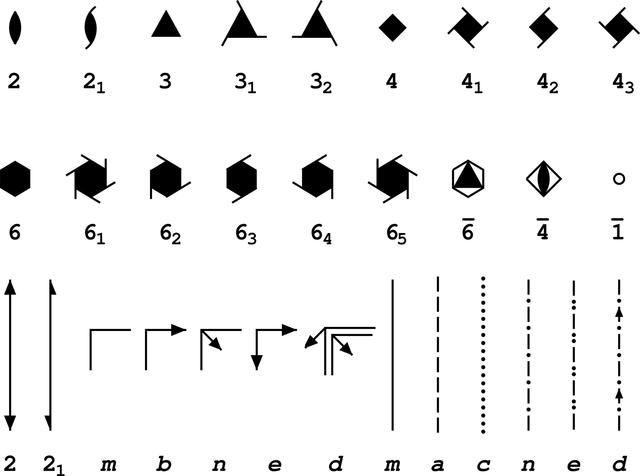
Image obtained from How to read (and understand) Volume A of International Tables for Crystallography: an introduction for nonspecialists [Dauter & Jaskolski (2010). J. Appl. Cryst. 43, 1150-1171, https://doi.org/10.1107/S0021889810026956]