Effects of Two-Fold Rotation Axes
Consider the space group diagram of \(P222\) below. The orange atom has been rotated \(180^{\circ}\) around the two-fold rotation axis located at \((\frac{1}{2}, \frac{1}{2}, c)\). This transforms it from its position of \((x, y, z)\) in fractional coordinates to a position of \((1-x, 1-y, z)\). However, due to the periodicity of the crystal, the coordinates \((1-x, 1-y, z)\) are identical to \((-x, -y, z)\). This is more commonly how this effect will be represented.
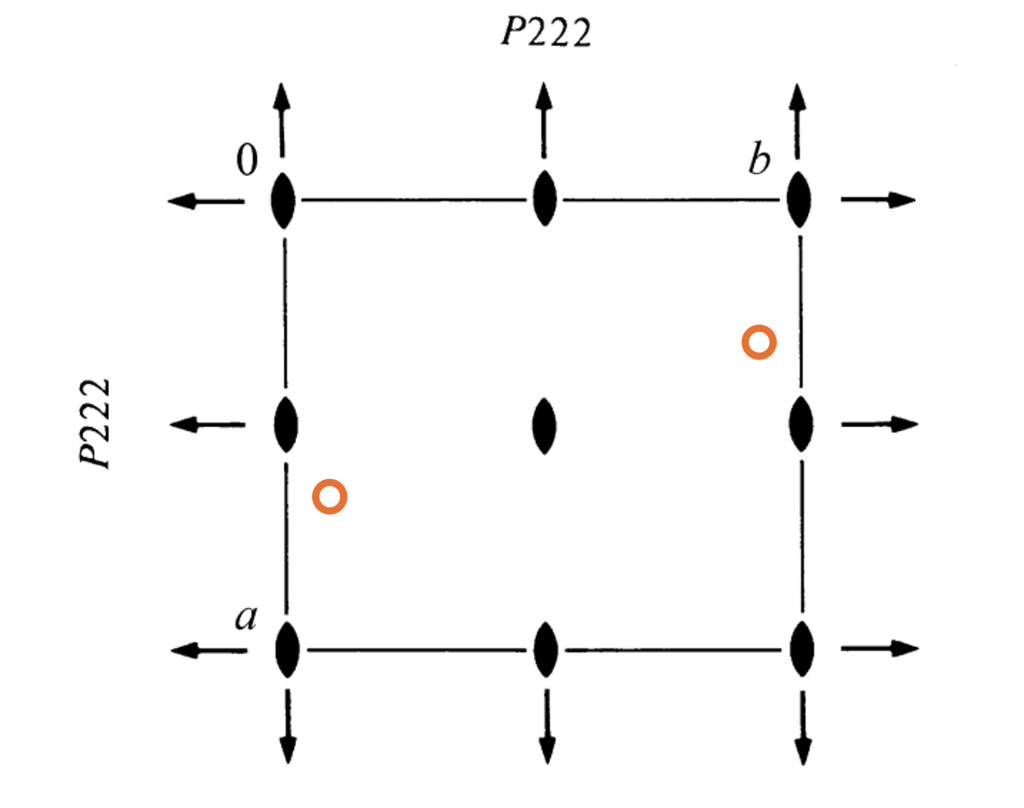
In fact, application of any of the two-fold rotation axes parallel to \(c\) will produce the same effect after periodicity of the crystal is applied. Have a go at drawing more than one unit cell of the diagram and rotating an atom around the different two-fold rotation axes.
The same effect will occur for two-fold rotation axes parallel to \(a\) and \(b\). The axis the rotation axis is parallel to will have its coordinate unchanged. A two-fold rotation parallel to \(b\) therefore transforms a point \((x, y, z)\) to the point \((-x, y, -z)\).
Position of the axis
The position of the rotation axes is important. In the above, the rotation axes were placed at \((0, 0, c)\) and its associated points. If the rotation axes were placed at \((\frac{1}{4}, 0, c)\) and associated points then the point \((x, y, z)\) is transformed to \((\frac{1}{2}-x, -y, z)\). In reality, the position of the axis should be doubled and added onto the coordinates made negative. This is the same as above for the rotation shown in the image. However, as mentioned, \((1-x, 1-y, z)\) is identical to \((-x, -y, z)\).
It is relatively simple to show that in orthorhombic unit cells a two-fold rotation axis at \((x, y, c)\) mandates a two-fold rotation axis at \((x + \frac{1}{2}, y + \frac{1}{2}, c)\). A rotation axis parallel to \(c\) at \((x, y, c)\) transforms the point \((h, k, l)\) to the point \((2x – h, 2y – k, l)\). This is identical to the point \((2x + 1- h, 2y + 1 – k, l)\) due to the periodicity of the lattice. A rotation axis at \((x + \frac{1}{2}, y + \frac{1}{2}, c)\) produces this second point and therefore must be present.