Effects of Mirror Planes
Unlike two-fold rotation axes, mirror planes only invert one coordinate. Symmetry elements are often defined in terms of the unique axis. For mirror planes in right-angled coordinate systems, definition of the plane is typically done as the axis it is perpendicular to. A plane is like a piece of paper held flat. There is only one line perpendicular to this piece of paper/plane. Therefore this is a simple way to define the position of a plane.
Below is the space group diagram of \(Pmmm\).
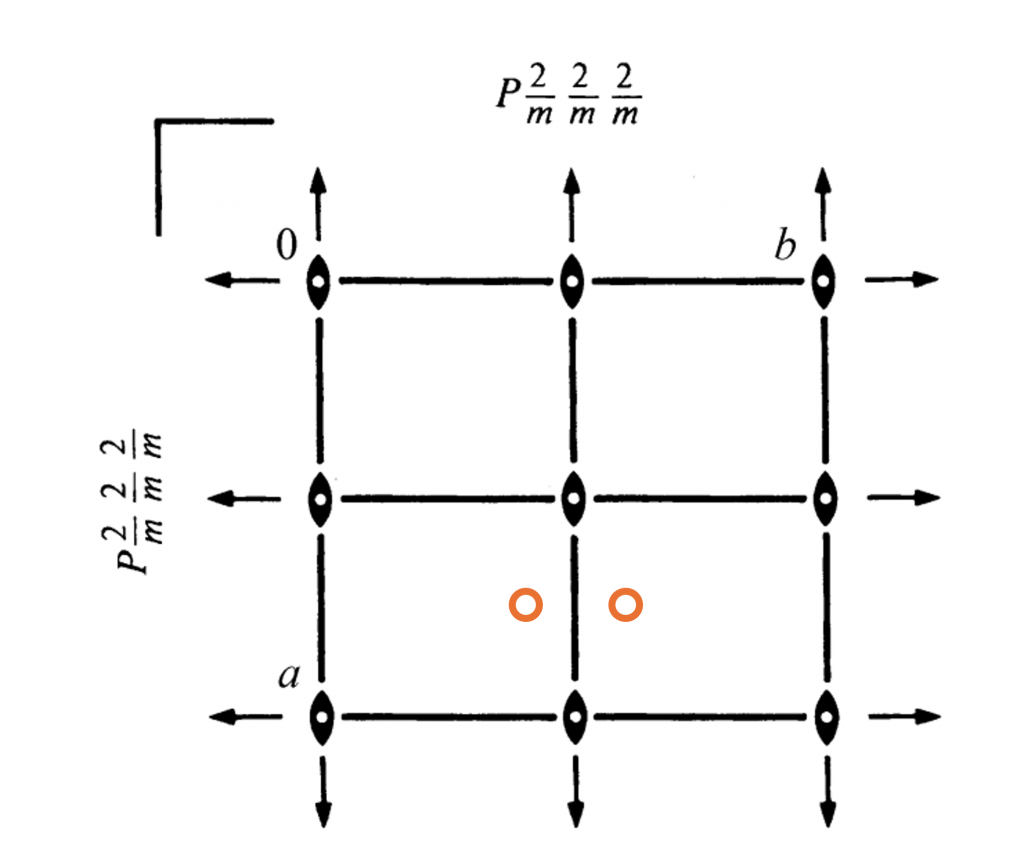
The orange atoms are reflections of one another. They are reflected through the mirror plane perpendicular to the \(b\) axis. If we were to use coordinates to represent these positions, atom 1 would be at \((x, y, z)\) with atom 2 at \((x, 1-y, z)\). The axis the mirror plane is perpendicular to, informs you about which coordinate is going to be made negative. As this mirror plane is perpendicular to the \(b\) axis, the \(b\) coordinate is made negative.
Position of the mirror plane
Just like the two-fold rotation axes, the position of the mirror plane affects the position where the atom finishes its transformation. The rule is the same as the two-fold rotation axes. Double the position of the plane and add it to the transformation. If a mirror plane perpendicular to the \(b\) axis is located at \((a, \frac{1}{4}, c)\), this will transform the atom at \((x, y, z)\) to the position \((x, \frac{1}{2} – y, z)\).
There is a simple derivation on the previous page showing that the presence of one two-fold rotation axis with periodic boundary conditions (the unit cell is repeated!) leads to multiple other two-fold rotation axes. This also applies to mirror planes.
The position of a mirror plane can be written as \((a, 0, c)\), as was done above. As only one coordinate need be defined (in our orthorhombic case), this is sometimes abbreviated to state that a mirror plane is present at \(b = 0\).