Understanding Coordinate Systems
In crystallography, cartesian coordinate systems (the ‘normal’ right-angled axes) are not often used. This is because the position of lattice points and symmetry elements are defined in terms of a fraction of the lattice vectors. For example, in orthorhombic space groups, the \(a\), \(b\) and \(c\) axes are different lengths. A two-fold rotation axis, in the standard setting of the lattice, might be present halfway along the \(a\) axis. Defining this position differently when your lattice vectors change size would be a tedious and unnecessary job. Instead, crystallographers use fractional coordinates. These are coordinates defined in terms of the lattice vectors. The image below shows the standard body-centred orthorhombic unit cell. Lattice points are observed at the positions \((0, 0, 0)\), \((0, 0, 1)\), \((0, 1, 0)\), \((1, 0, 0)\), \((0, 1, 1)\), \((1, 0, 1)\), \((1, 1, 0)\), \((1, 1, 1)\) and \((\frac{1}{2}, \frac{1}{2}, \frac{1}{2})\). If the \(c\) axis grows longer, the lattice points still remain at their position in fractional coordinates.
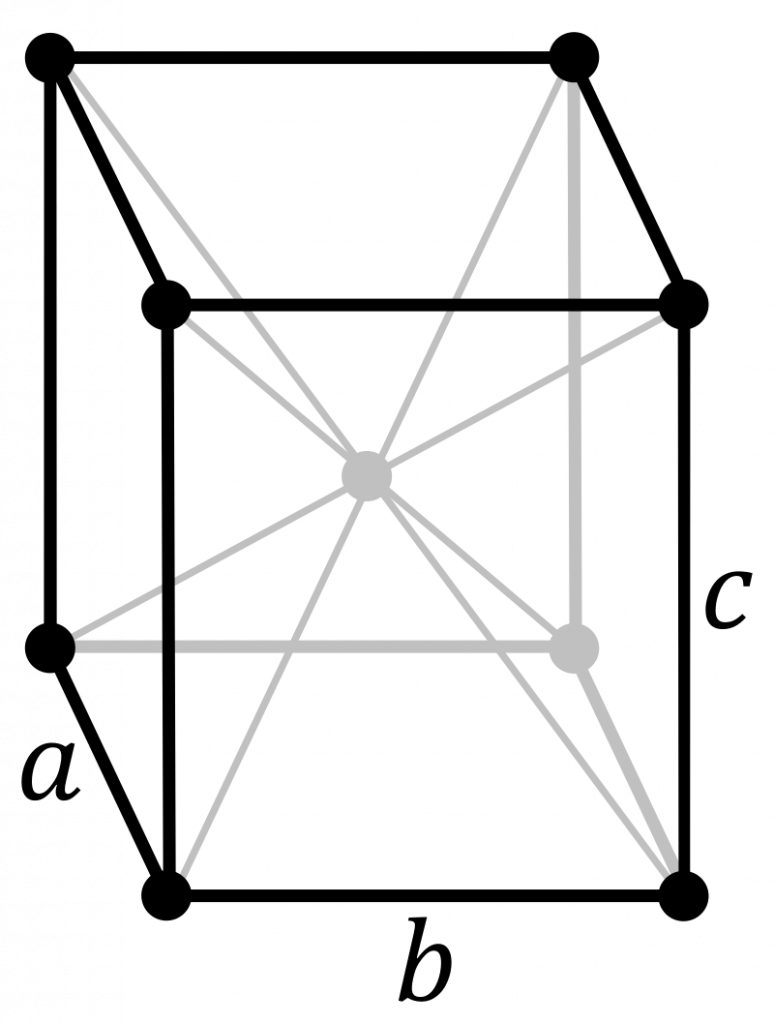
The use of fractional coordinates also makes the translational symmetry of the lattice neater, as coordinates never need be below 0 or above 1. The lattice points listed above can actually be reduced to just \((0, 0, 0)\) and \((\frac{1}{2}, \frac{1}{2}, \frac{1}{2})\). The point \((0, 0, 1)\) is identical to the point \((0, 0, 0)\).
When the unit cell axes are perpendicular, convert between fractional and cartesian coordinates as follows: $$ a = \frac{x}{|\mathbf{a}|}$$ $$ b = \frac{y}{|\mathbf{b}|}$$ $$ c = \frac{z}{|\mathbf{c}|}$$
This course will begin by dealing with the effect of symmetry elements on positions in orthorhombic unit cells represented in fractional coordinates. The teachings here can be simply applied to tetragonal and cubic space groups. Other coordinate systems (non-perpendicular axes) will be dealt with later once the basics are established in right-angled axes.