Monoclinic Unit Cells
The monoclinic unit cell, viewed along the \(b\) axis can be taken as a more general form of the approach taken to hexagonal coordinates on the previous page. Have a go at drawing out this unit cell and working out the equations for conversion between the monoclinic and cartesian coordinates. Place the origin at the lattice point in the bottom left. The equations are given below.
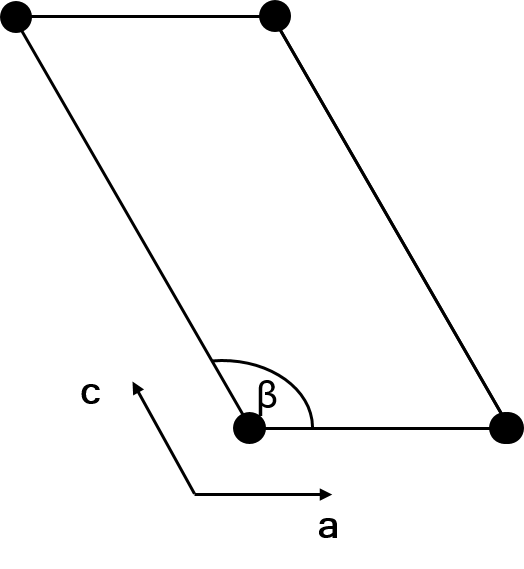
This can be determined by drawing a similar triangle to that for the hexagonal coordinate system. \(x\), \(y\) and \(z\) are used in the 2D orientation shown (\(x\) points right, \(y\) points up and \(z\) is coming out of the page).
$$x = a – c \cos (180^{\circ} – \beta) = a + c \cos (\beta)$$
$$y = c \sin (180^{\circ} – \beta) = c \sin (\beta)$$
$$z = b$$
For those interested in some of the extra maths-y bits of symmetry elements and coordinates, a short course is also provided on this site which should enhance your skills and understanding of the maths behind much of the following content.