Hexagonal Coordinates
Orthorhombic space groups were dealt with initially in order to introduce the use of coordinates for symmetry elements and atomic positions. Other crystal systems with non-perpendicular axes complicate the use of coordinates. Lattice vectors are no longer perpendicular, though every position in the unit cell can still be defined in terms of the lattice vectors. Consider the red atom in the unit cell of $P3$ (a trigonal space group) below. To determine the coordinates in terms of the lattice vectors, the route from the origin is along the arrow labelled a, then along the arrow labelled b. This can be done for any position in the unit cell.
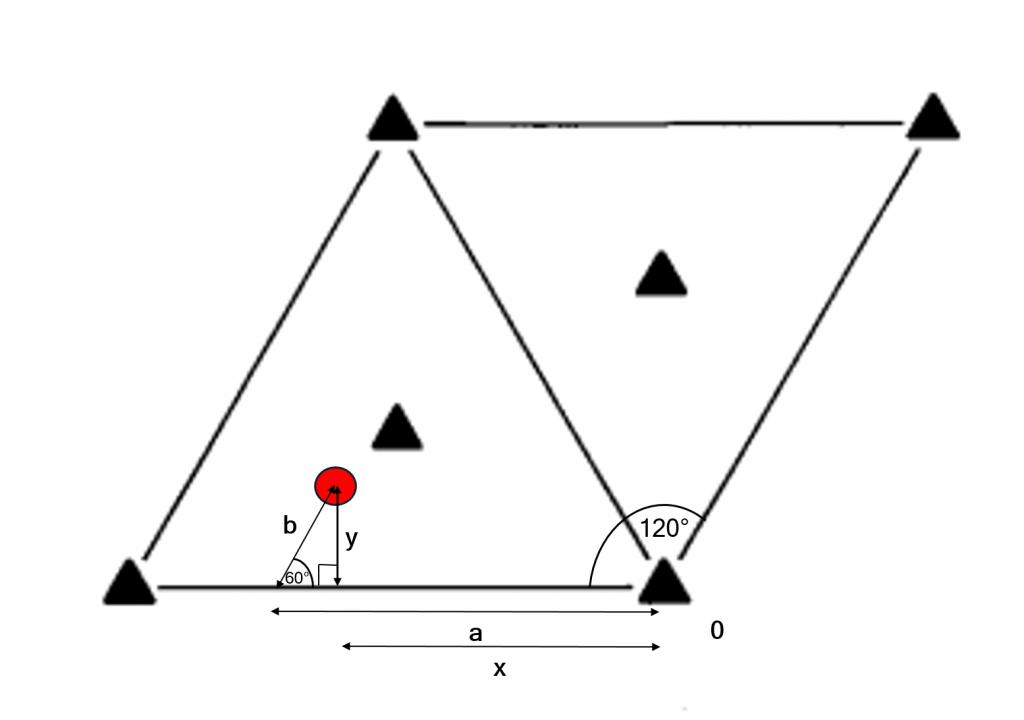
In the trigonal and hexagonal crystal systems, the angle between the \(a\) and \(b\) axes is \(120^{\circ}\). Cartesian (right-angled) coordinates can be determined using trigonometry with the triangle depicted in the image above. Other triangles can be drawn to solve this problem.
$$x = a – b \cos (60^{\circ})$$
$$y = b \sin (60^{\circ})$$
$$z = c$$
These equations are not often used, but can come in handy in the derivation of atomic positions. Understanding these coordinate systems will be useful to understand the effect of higher order rotation axes.
In The International Tables the coordinates given for trigonal and hexagonal space groups will be in the hexagonal coordinate system, not cartesian.
Remember that the \(a\) and \(b\) axes are of equal length in the conventional trigonal and hexagonal unit cells.