Understanding Tetragonal Space Group Symbols
Tetragonal space group symbols give symmetry elements with unique axis \(\mathbf{c}\), \(\mathbf{a}\) and \(\mathbf{a}-\mathbf{b}\) respectively. Below is the space group diagram of \(P4bm\).
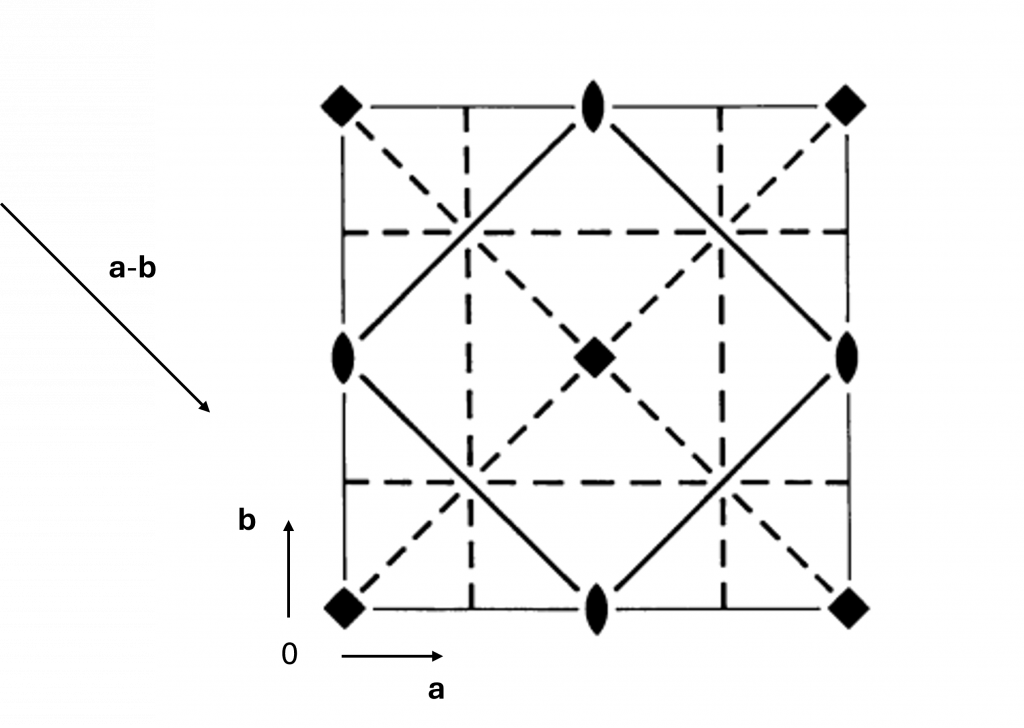
The vector \(\mathbf{a}-\mathbf{b}\) is also shown. The key symmetry elements from the short space group symbol are the four-fold rotation axis parallel to \(c\), the \(b\) glide perpendicular to \(a\) and the mirror plane perpendicular to the vector \(\mathbf{a}-\mathbf{b}\).
Other symmetry elements are present, but can be derived from the base symmetry shown in the space group symbol. For example, there is a glide plane perpendicular to \(\mathbf{a}-\mathbf{b}\) with glide vector of \(\mathbf{a}+\mathbf{b}\).
This glide plane is actually a combination of the mirror plane shown, the \(a\) glide perpendicular to \(b\) and the \(b\) glide perpendicular to \(a\).