Subgroups and Supergroups
It should be noted that it is possible to build a structure in crystallographic programs like CrystalMaker or VESTA that has the space group \(Pnma\) in a \(P1\) unit cell. This simply requires placing atoms at the general positions associated with \(Pnma\). In some senses, every other space group can be thought of as special cases of \(P1\). For example, orthorhombic lattices are a special case of the triclinic lattice where the angles of the parallelepiped equal \(90^{\circ}\).
This leads us to relationships between different space groups and the concept of subgroups and supergroups. These relations are useful to understand as it can be common for phase transitions to change the symmetry from one group to another related group.
A subgroup of a group is a group which has lost symmetry compared to the original group. For example, \(Pm\) is a subgroup of \(Pmm2\). This is achieved by removal of one of the mirror planes and the two-fold rotation axis. It is not possible to remove only one symmetry element from \(Pmm2\) as the two mirror planes produce the two-fold rotation (and a two-fold rotation and parallel mirror plane produce the other mirror plane!).
A supergroup is the opposite, in which symmetry is added. As such, \(Pmm2\) is a supergroup of \(Pm\).
Crystallographic Point Groups
Crystallographic point groups denote the symmetry of the crystal without any translational symmetry. As such, space groups such as \(Pmna\) have a point group \(mmm\) as each of the glide planes become mirror planes when translation is ignored. Centring is also ignored as this is a translation effect. Similarly, \(P\bar{3}1c\) would have \(\bar{3}1m\) as its crystallographic point group.
This will be important as we learn more about subgroups and supergroups.
Relationships between groups
Group relations are usually given as maximal subgroups and minimal supergroups. This terminology simply means that there is no group between the group of interest and the sub-/supergroup. There can be multiple of these, depending on what symmetry is lost, but there is no intermediate group. One can thus build up a ‘tree’ depicting group relations over more ‘branches’. This tree can get complicated if showing all 230 space groups (every group is a supergroup of \(P1\)), hence the use of minimal and maximal super-/subgroups.
The image shows some of the possible ways of symmetry descent from \(P4/mbm\). Note that when removing two ‘layers’ of symmetry, this can be achieved in multiple ways.
Translationengleiche
‘Translationengleiche’ translated from German literally means ‘translations same’. This refers to sub-/supergroups in which the translational symmetry is identical. As such, the centring of the unit cell, and the size of the unit cell must be identical. If the size or centring of the unit cell changed, this corresponds to a change in translational symmetry!
The example above of \(Pmm2\) and \(Pm\) is an example of a translationengleiche sub-/supergroup relationship.
Below is an image of some of the translationengleiche subgroups of \(P\frac{4_{2}}{m}bm\). This is the ‘tree’ described above. Those in the first layer from the top are the maximal translationengleiche subgroups. Those in the second or higher layer are general subgroups. While there is only one route to each maximal subgroup (as there must be!), there can be multiple routes to the other general subgroups. It may seem peculiar to see translationengleiche subgroups such as \(Cmmm\) present in this tree. It is important to consider the structure as a whole, not just the unit cell. The image below the tree is taken directly from The International Tables.
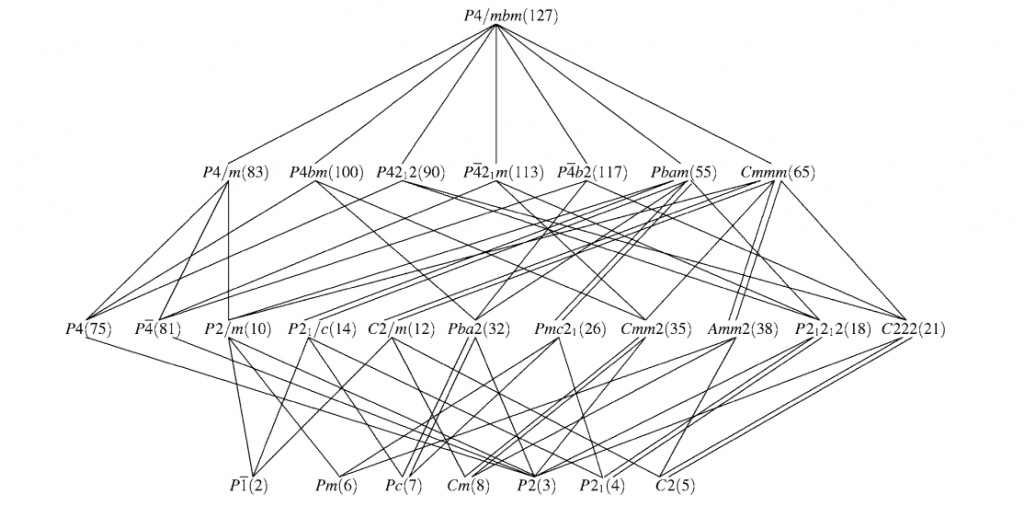

This shows the maximal translationengleiche subgroups. On the left, it initially defines the symmetry in the original notation used for tetragonal space groups. Check out where it says \(P\frac{2}{m}1\frac{2}{m}\). This corresponds to the removal of the \(b\) glide perpendicular to \(a\) (which forces removal of the four-fold rotation also). If a re-definition of the axes is performed, such that \(\mathbf{a’} = \mathbf{a} – \mathbf{b}\) and \(\mathbf{b’} = \mathbf{a} + \mathbf{b}\), this is identical to the orthorhombic space group \(Cmmm\). This axis re-definition is shown in The International Tables.
In terms of the overall structure, no translations have been removed. This translational symmetry was already present within the space group \(P\frac{4_{2}}{m}bm\).
Klassengleiche
‘Klassengleiche’ means ‘same class’. This refers to a situation in which the crystallographic point group has remained the same. As a result, the group must have lost translational symmetry.
Isomorphic
Isomorphic subgroups refer to a subgroup in which the space group symbol remains identical or in the enantiomorphic space group. Enantiomorphic simply refers to space groups that are related by mirroring, such as \(P3_{1}\) and \(P3_{2}\). This may sound strange, but it is possible to lose translational symmetry and remain in the same space group. Consider the hexagonal lattices below.
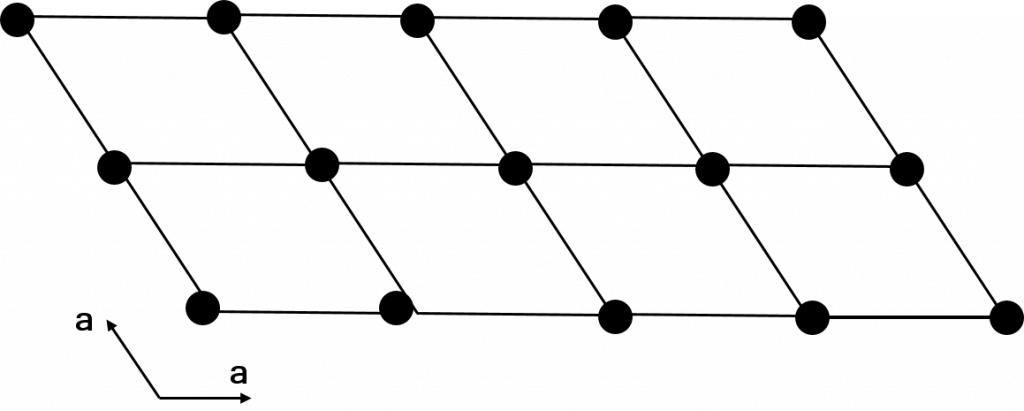
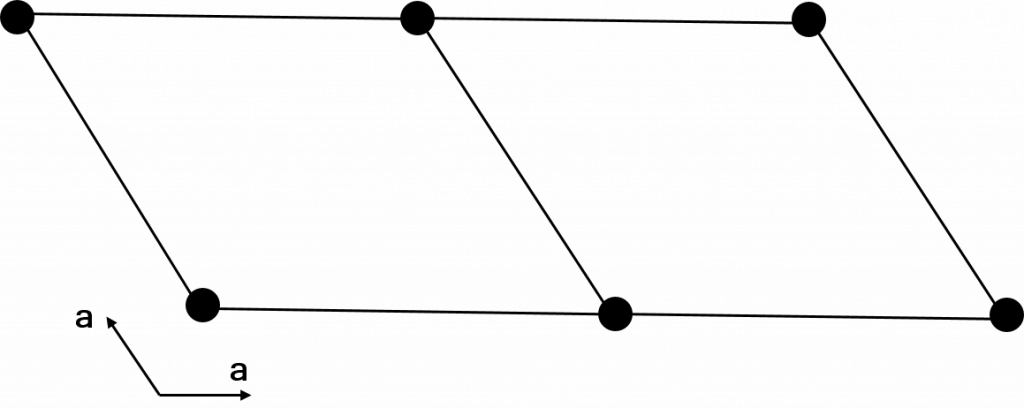
If we place only half the lattice points as shown on the right of the above image, this corresponds to an increase of the unit cell size. The space group symbol will remain the same, yet we have indeed lost translational symmetry from the overall structure.
This is the concept of isomorphic subgroups. Maximal isomorphic subgroups refer to these sort of unit cell size changes in which the size is increased by a prime number factor. As such, there are as many of these as there are prime numbers (infinitely many!). The reason only prime number increases are maximal subgroups is simple. Consider a \(Pmna\) unit cell. An isomorphic subgroup of this would be one in which the conventional unit cell is now defined by \(\mathbf{a’} = \mathbf{a}\), \(\mathbf{b’} = \mathbf{b}\) and \(\mathbf{c’} = p\mathbf{c}\). If \(p = 6\), this could be achieved by first going through a unit cell double the size, then going through a unit cell three times the size of the new unit cell (\(3 \times 2 = 6\)). This means there is an intermediate group between the subgroup and original group, and thus the case of \(p = 6\) is not a maximal subgroup. This is the case for any \(p\) that is not prime.
As there are infinitely many of these for each group, they are not listed in The International Tables. They simply refer to enlargements of the unit cell, which in itself is a loss of translational symmetry.
Non-isomorphic – Loss of Centring
A simple example of non-isomorphic klassengleiche subgroups is that in which the translational symmetry of centring is lost. For example, \(Pmm2\) is a maximal non-isomorphic klassengleiche subgroup of \(Cmm2\). This is relatively simple to understand given what we have learned.
Non-isomorphic – Enlarged Unit Cell
These can often appear counterintuitive. For example, \(C222\) can actually be a subgroup of \(P222\) if the unit cell is enlarged. However, \(P222\) is clearly a subgroup of \(C222\) when the unit cell remains the same size. This cuts to the crux of understanding the details of klassengleiche subgroups and supergroups. The full structure (not just the unit cell!) must be looked at in order to determine whether symmetry has descended or ascended.
Consider the primitive orthorhombic structure shown below (left).
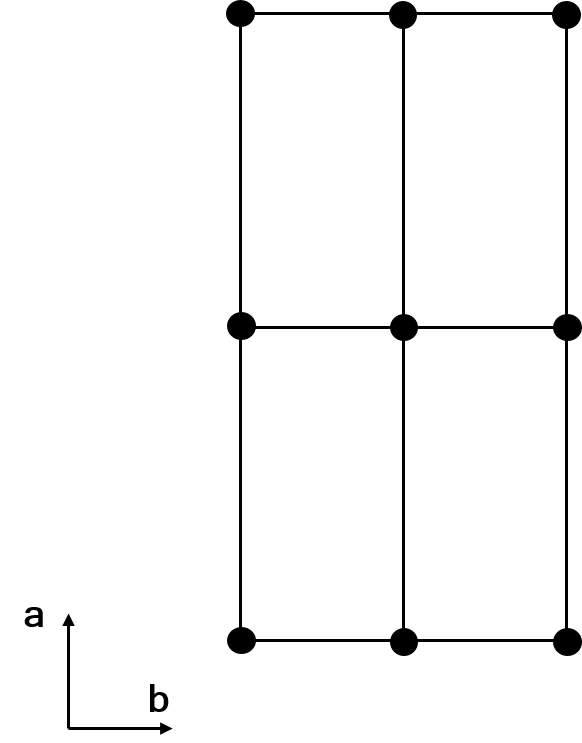
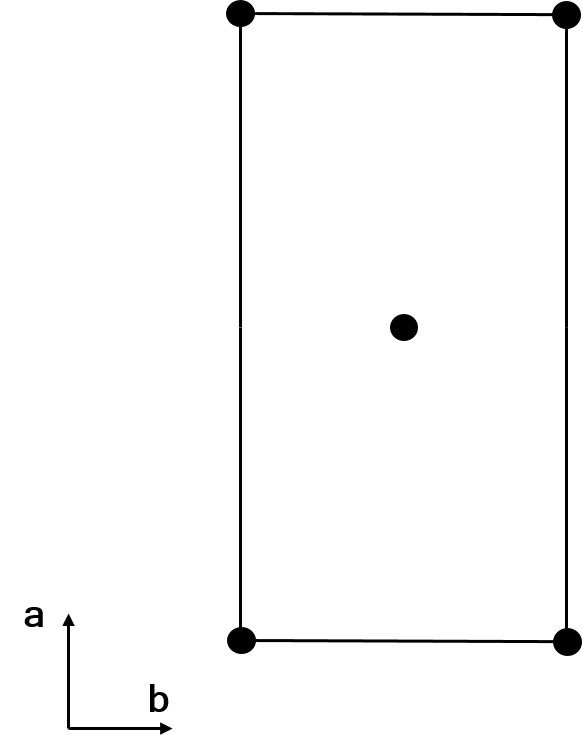
If certain lattice points are removed from the structure as a whole, then the new unit cell of the structure is as shown on the right of the image above. This is a \(C\)-centred cell! Again, we have lost translational symmetry when the structure as a whole is considered, despite the space group symbol appearing to ascend in symmetry.