Symmetry Requirements of Monoclinic
It can be easier to see this in two-dimensions initially. This is not a rigorous mathematical proof, but can be seen as an intuitive demonstration of why introducing a mirror plane (or rotation axis) to the lattice places restrictions on the unit cell.
Consider a 2D lattice made of parallelogram unit cells (the 2D equivalent of a parallelepiped) as below:
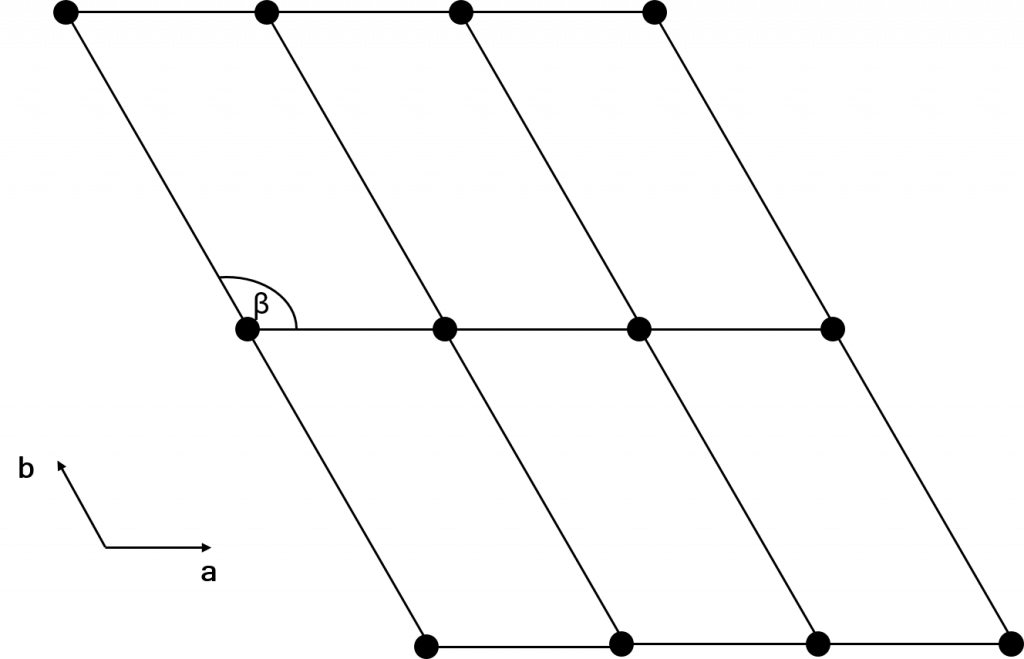
Now let’s introduce a mirror plane along the b axis, shown in orange in the image below. If the lattice points on the left are reflected in the mirror plane, they move to the orange positions shown. This changes the lattice, and as such this mirror plane cannot exist in this lattice.
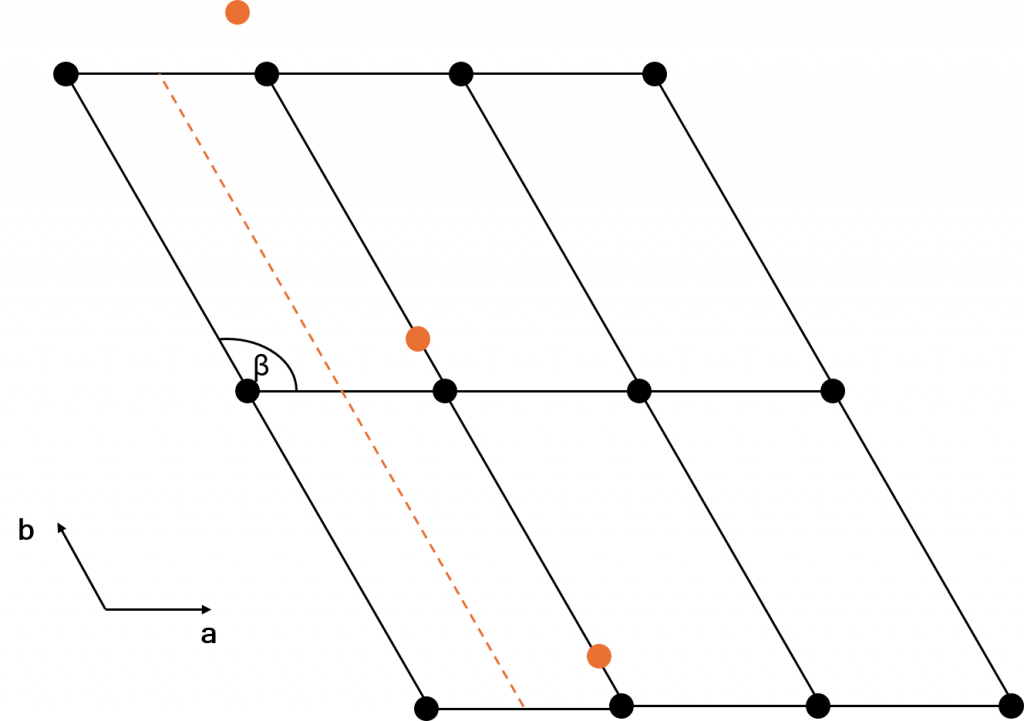
While this is a simple demo of only one mirror plane, you are welcome to attempt to find another mirror plane that will work with this lattice as given (you shouldn’t be able to though!).
The mirror plane shown above will only map the orange points onto pre-existing lattice points if the angle \(\beta \) is \(90 ^{\circ}\), as shown below.
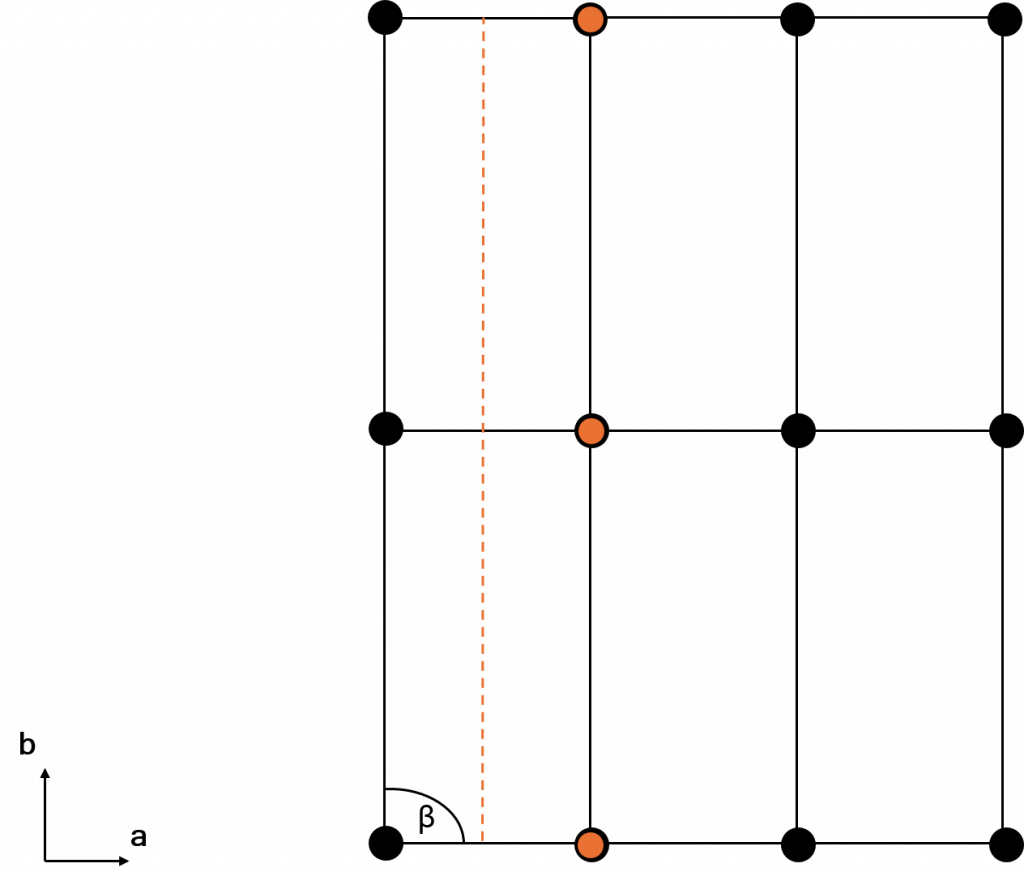
While shown for 2D plane groups here, the concept is the same for the monoclinic and orthorhombic unit cells in 3D.