Hexagonal-Rhombohedral Conversions
Seeing the conversion between rhombohedral and hexagonal unit cells is very tricky. While they are presented here, the best method to really understand this is to open up a crystal visualisation software like CrystalMaker or VESTA.
A hexagonal lattice is equivalent to a rhombohedral unit cell with lattice positions at \((0, 0, 0), (\frac{1}{3}, \frac{1}{3}, \frac{1}{3})\) and \((\frac{2}{3}, \frac{2}{3}, \frac{2}{3})\). If you view multiple rhombohedral unit cells with these lattice points, you might be able to pick out the primitive hexagonal cell.
Similarly, a rhombohedral lattice is equivalent to a hexagonal unit cell with lattice positions at \((0, 0, 0), (\frac{2}{3}, \frac{1}{3}, \frac{1}{3})\) and \((\frac{1}{3}, \frac{2}{3}, \frac{2}{3})\). Viewing multiple hexagonal unit cells with these lattice points might allow you to pick out the primitive rhombohedral cell.
This is how the images below were produced. On the left is the first example (hexagonal lattice in a rhombohedral cell), and the right is the second example (rhombohedral lattice in a hexagonal cell). The primitive unit cells are shown as thick bonds between the lattice points.
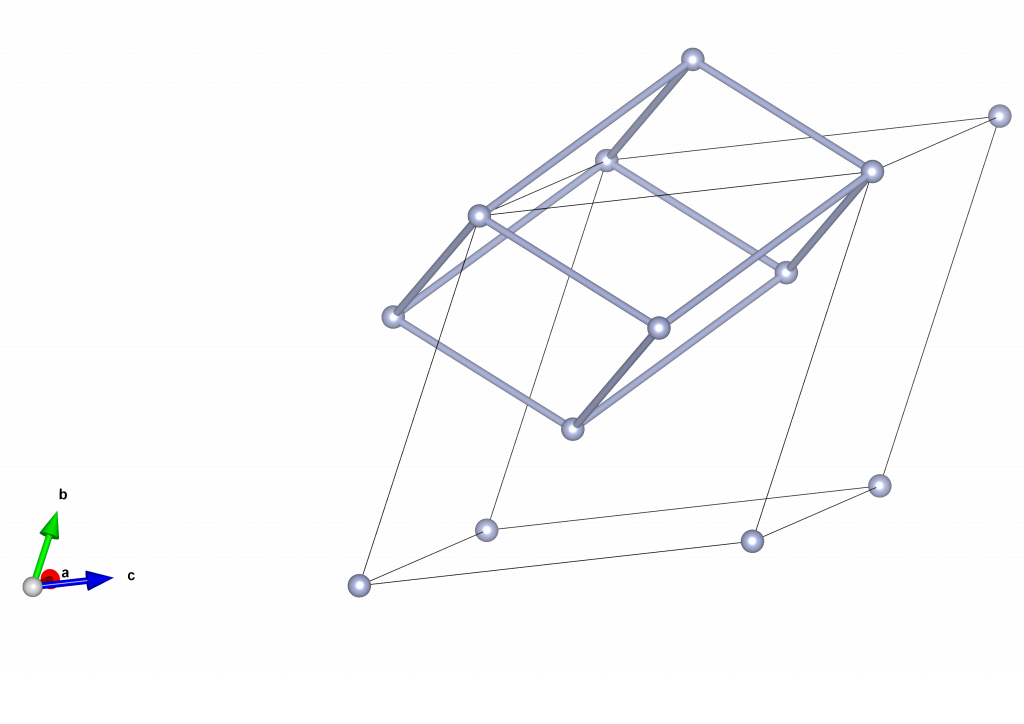
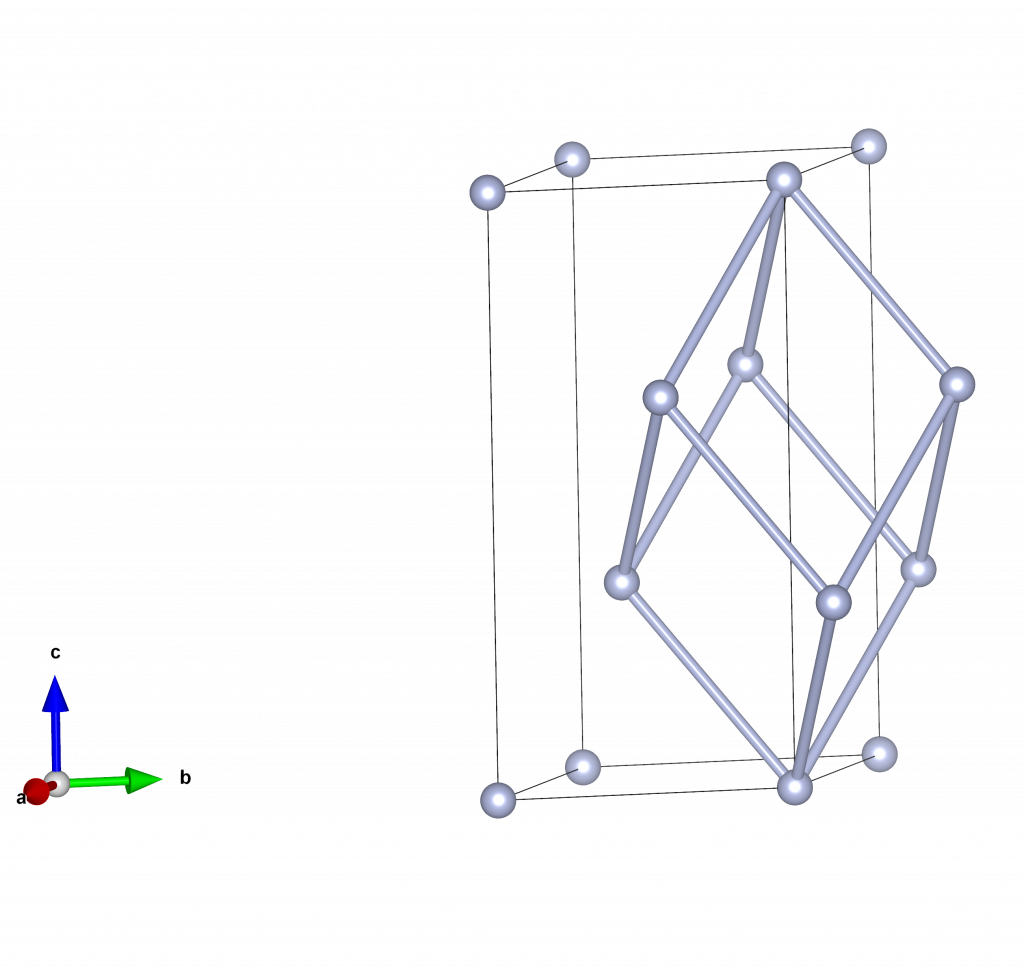
If you would like to try this yourself, allowing visualisation in 3D, download VESTA (https://jp-minerals.org/vesta/en/download.html) and follow the below instructions:
- Open VESTA and click File -> New Structure
- Click the ‘Unit Cell’ tab and change the ‘System’ to Trigonal. The ‘Space Group’ should automatically change to ‘P3’, but do this yourself if it doesn’t.
- In the ‘Unit Cell’ tab, change the lattice parameters to \(a = 5\) and \(c = 3.3\). All hexagonal lattices have an associated rhombohedral unit cell, but I have chosen these lattice parameters to help visualise them and the angles between the rhombohedral lattice vectors.
- Click the ‘Structure Parameters’ tab. Click ‘New’ to produce a new atom. Change the symbol and label to ‘C’. Leave the x, y, z values as 0. Repeat this process, changing the x, y, z coordinates to \((\frac{2}{3}, \frac{1}{3}, \frac{1}{3})\) and \((\frac{1}{3}, \frac{2}{3}, \frac{2}{3})\). You should now have 3 carbon atoms in your hexagonal unit cell, representing the lattice points of a rhombohedral lattice in a hexagonal unit cell. Click ‘OK’.
- Click ‘Edit’ -> ‘Bonds’. Click ‘New’. Set up a bond between two carbon atoms with a maximum distance of 3.1 Angstroms. Click ‘OK’.
- You should now see bonds between the carbon atoms. These bonds are the rhombohedral unit cell vectors. Try to pick out a parallelepiped that represents the rhombohedral unit cell. The original hexagonal unit cell should be shown as a thin black outline.
- You can rotate the structure by clicking and dragging your mouse. You can extend the size of the structure by adjusting the number of unit cells shown. Do this by clicking ‘Objects’ -> ‘Boundary’ and adjusting the minima and maxima of x, y, and z.