Effects of Lattice Point Centring
Lattice point centring also produces identical positions within a unit cell. In the orthorhombic crystal system, there are four types of lattice centring, shown below. From left to right, these are primitive (\(P\)), face-centred (\(F\)), body-centred (\(I\)) and base-centred (\(A\), \(B\) or \(C\)).
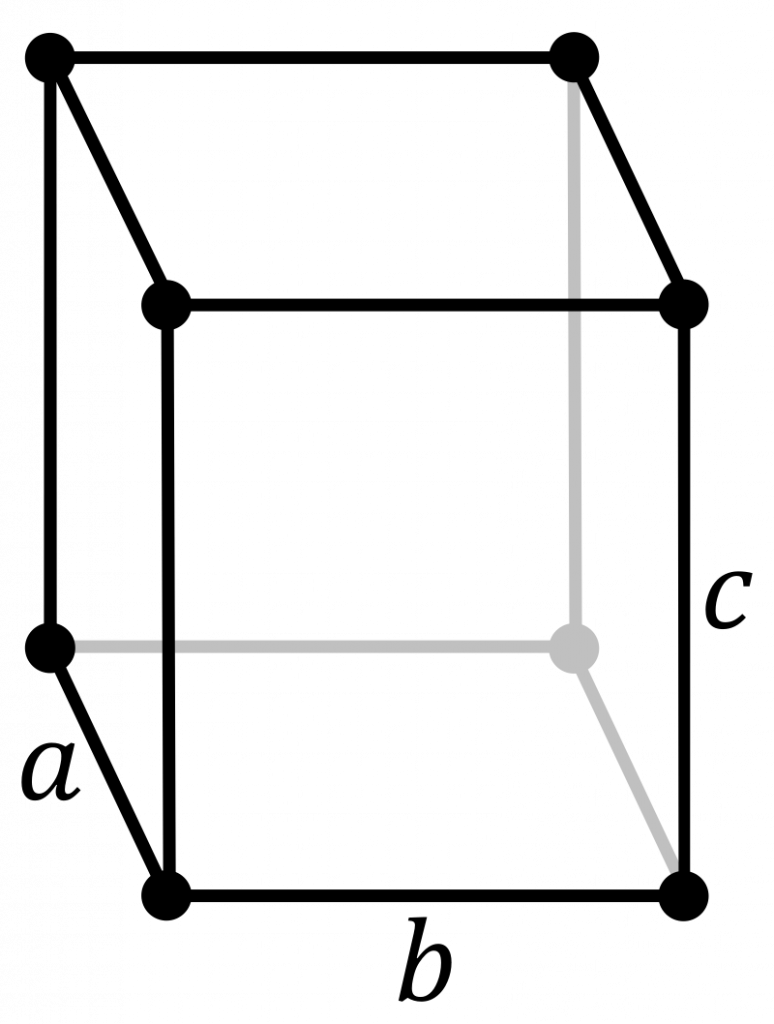
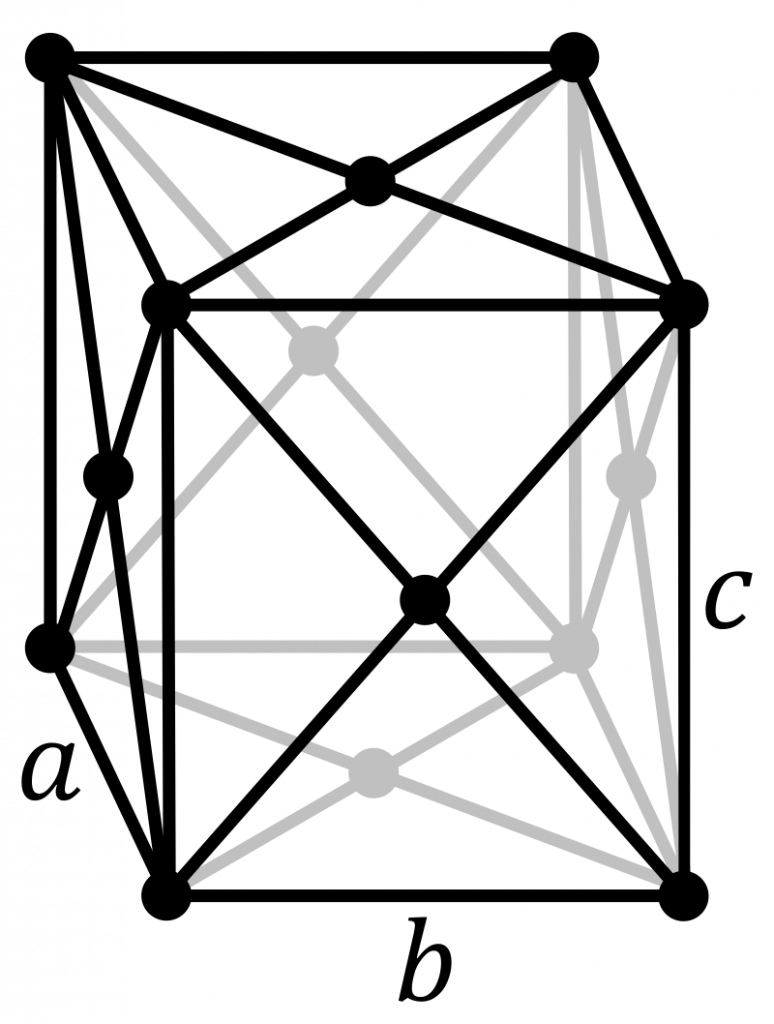
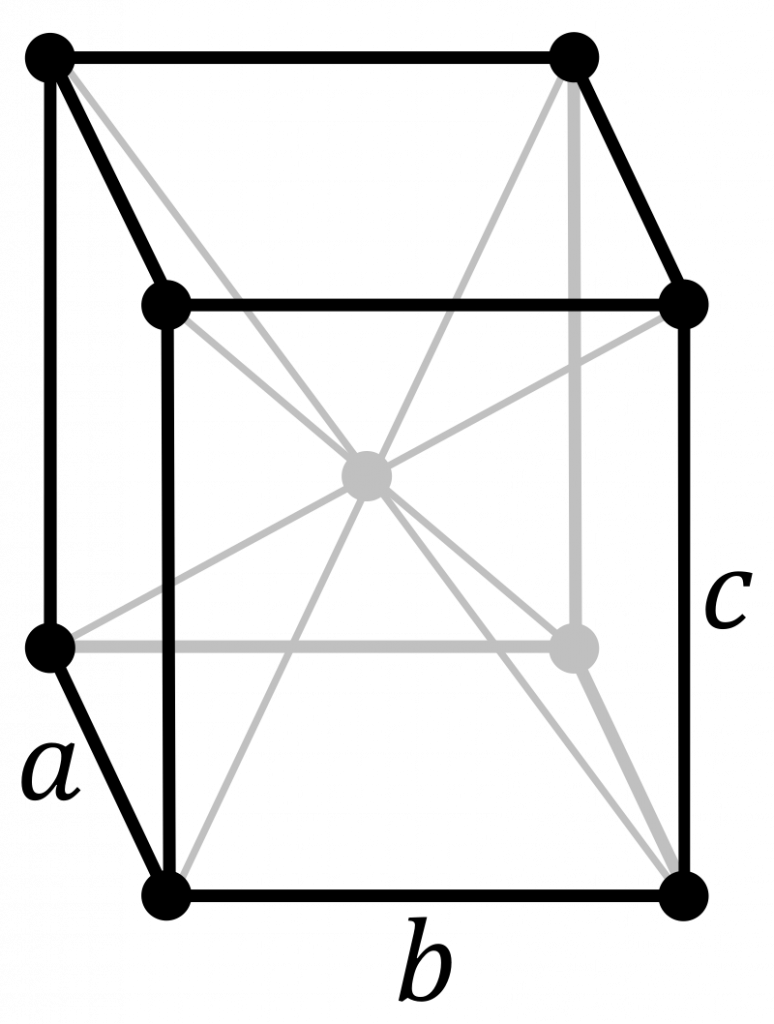
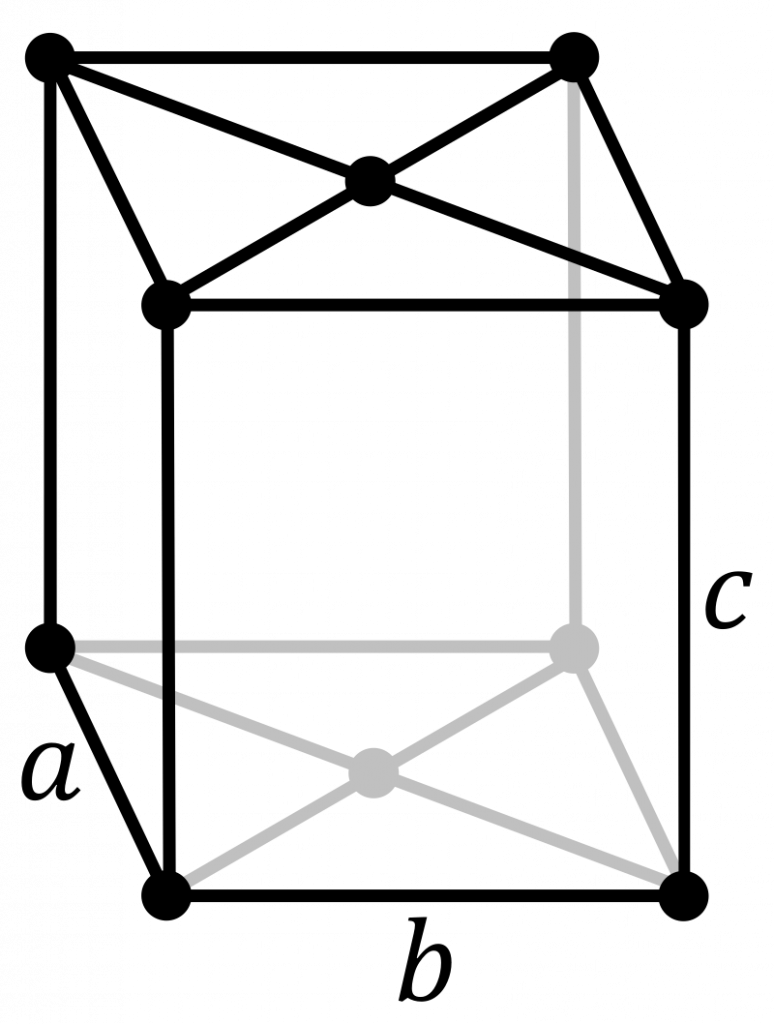
Primitive lattice centring places lattice points at the vertices of the unit cell. This is the same as the position \((x, y, z)\) being identical to \((x + 1, y+1, z+1)\). These are the usual periodic conditions of the unit cell.
Face-centred orthorhombic lattices have an extra lattice point on each face of the unit cell. Therefore, the positions of the lattice points in the conventional unit cell are \((0, 0, 0)\), \((0, \frac{1}{2}, \frac{1}{2})\), \((\frac{1}{2}, 0, \frac{1}{2})\), \((\frac{1}{2}, \frac{1}{2}, 0)\). Treating this as a symmetry element, position \((x, y, z)\) is identical to the positions \((x, y+\frac{1}{2}, z+\frac{1}{2})\), \((x+\frac{1}{2}, y, z+\frac{1}{2})\), \((x+\frac{1}{2}, y+\frac{1}{2}, z)\)
Body-centred orthorhombic lattices has position \((x, y, z)\) identical to the position \((x+\frac{1}{2}, y+\frac{1}{2}, z+\frac{1}{2})\). This is relatively easy to see from the image above.
Base-centred lattices have an extra lattice point on one of the faces of the conventional unit cell. As with rotation axes and mirror planes, this is defined by the unique axis. \(A\)-centred lattices have an extra lattice point on the unit cell face perpendicular to the \(a\) axis. Shown in the image is a \(C\)-centred lattice, as the face perpendicular to the \(c\) axis has the extra lattice point.
\(A\)-centred lattices thus have position \((x, y, z)\) identical to the positions \((x, y+\frac{1}{2}, z+\frac{1}{2})\). \(B\)-centred lattices have position \((x, y, z)\) identical to the positions \((x+\frac{1}{2}, y, z+\frac{1}{2})\). \(C\)-centred lattices have position \((x, y, z)\) identical to the positions \((x+\frac{1}{2}, y+\frac{1}{2}, z)\).