Bravais Lattices – The Cubic Lattices
Cubic lattices have four three-fold axes of rotation. These axes are oriented perfectly between the x, y and z vectors of cartesian coordinates. They pass through opposite faces of an octahedron, hence there are four of these axes (octahedrons have eight faces). As these three-fold rotation axes exchange the x, y and z directions, all three axes of the conventional unit cell are equal and all angles are \(90 ^{\circ}\). The conventional unit cells are therefore all cubes, hence the name. Cubic lattices have only one parameter free to vary, a, the length of the cube. Shown below is the primitive, body-centred and face-centred unit cells.
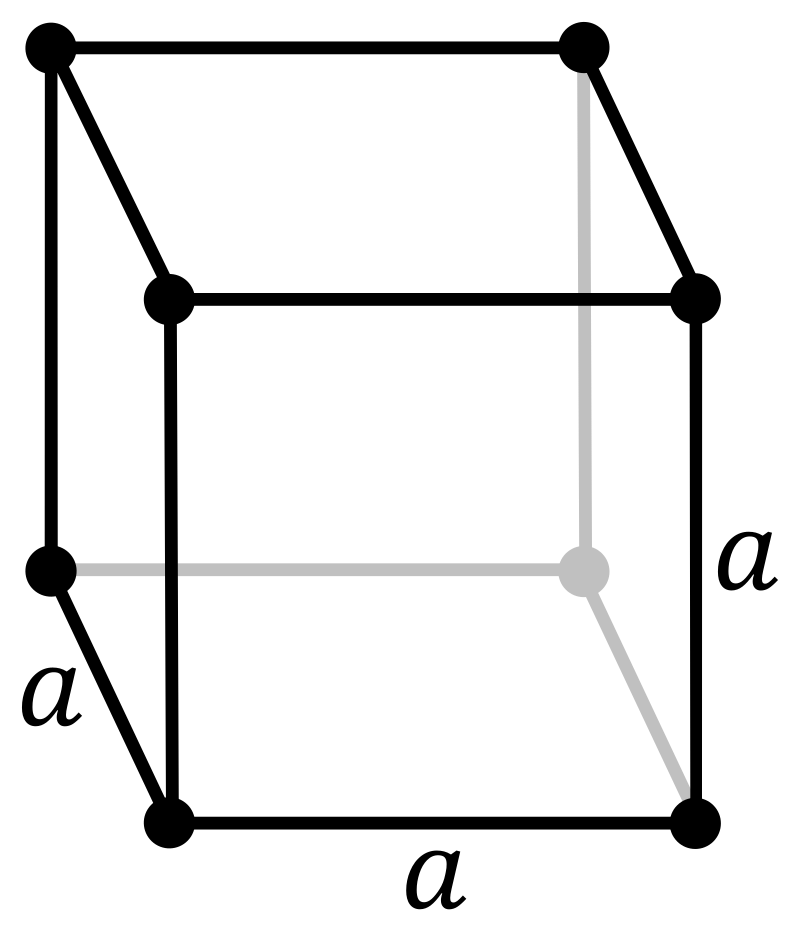
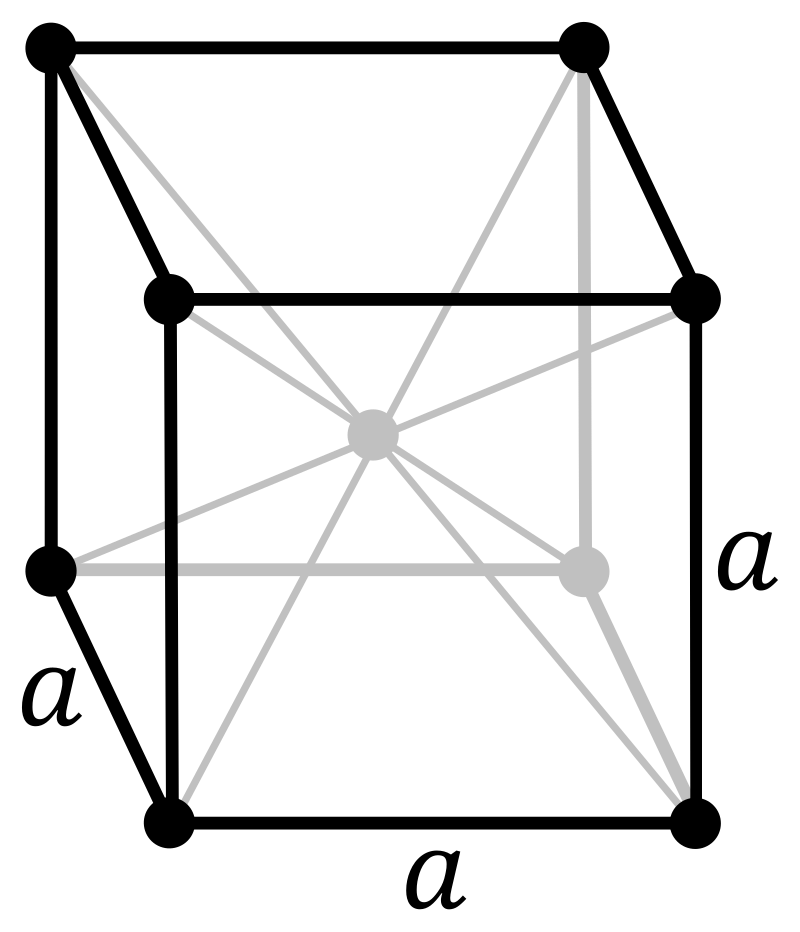
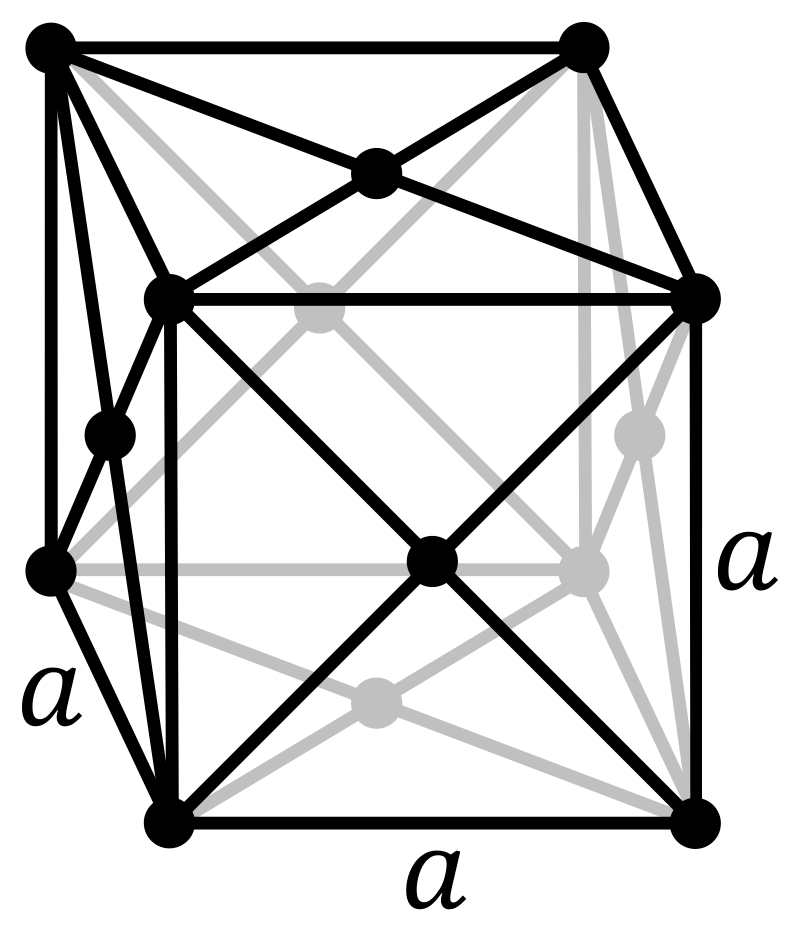
Base-centred unit cells cannot exist in cubic symmetry, as this would break the three-fold rotation axes which exchange the x, y and z directions (x, y and z are no longer equivalent in a base-centred unit cell).