Bravais Lattices – The Orthorhombic Lattices
As seen in the monoclinic crystal system, the symmetry imposed requirements on the unit cell. The orthorhombic crystal system has three two-fold rotation axes or one two-fold rotation axis and two mirror planes. In a similar way to the monoclinic crystal system, there must be a unit cell representing the lattice with \(\alpha\), \(\beta\) and \(\gamma\) angles of \(90^{\circ}\), because of these symmetry requirements. These are the conventional unit cells. These can all be converted to primitive unit cells with different shapes, if desired.
The orthorhombic crystal system makes use of all four typical lattice point arrangements: primitive, base-centred, body-centred and face-centred. None of these unit cells are identical, as they were shown to be for the monoclinic crystal system. These are shown from left to right in the image below.
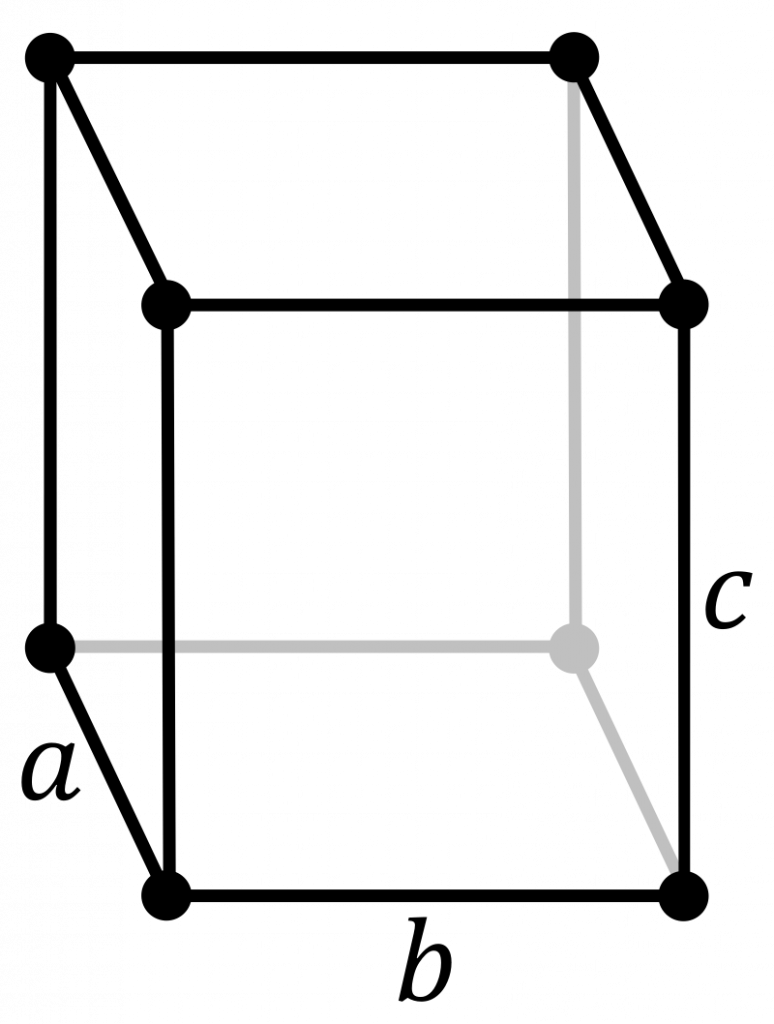
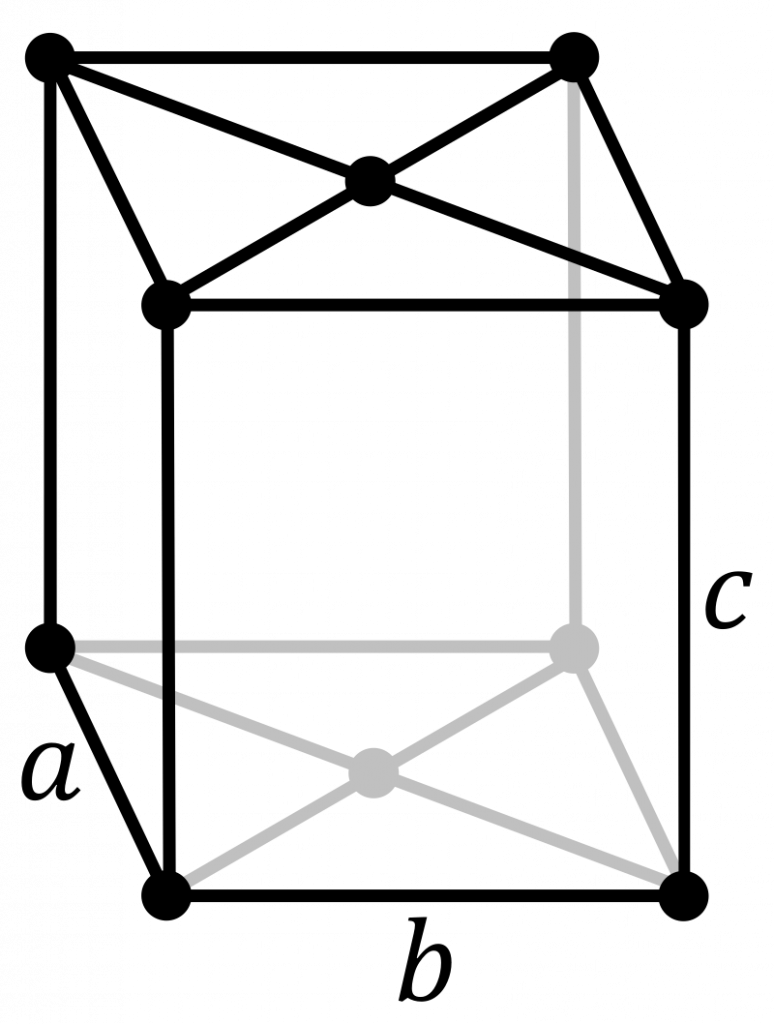
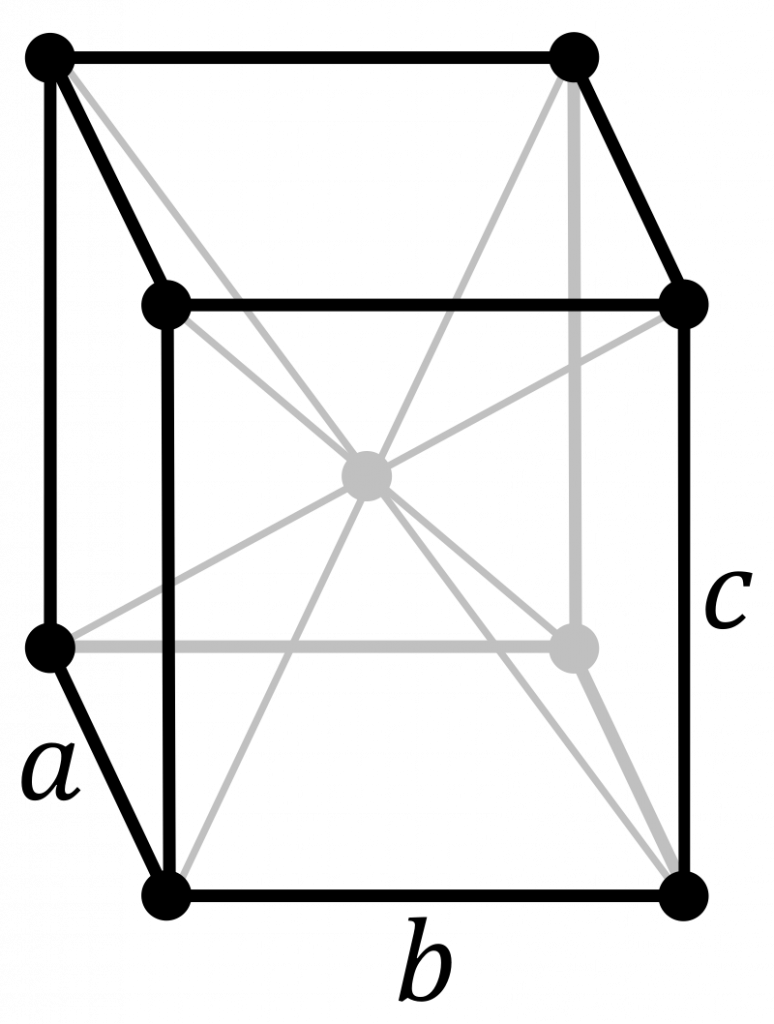
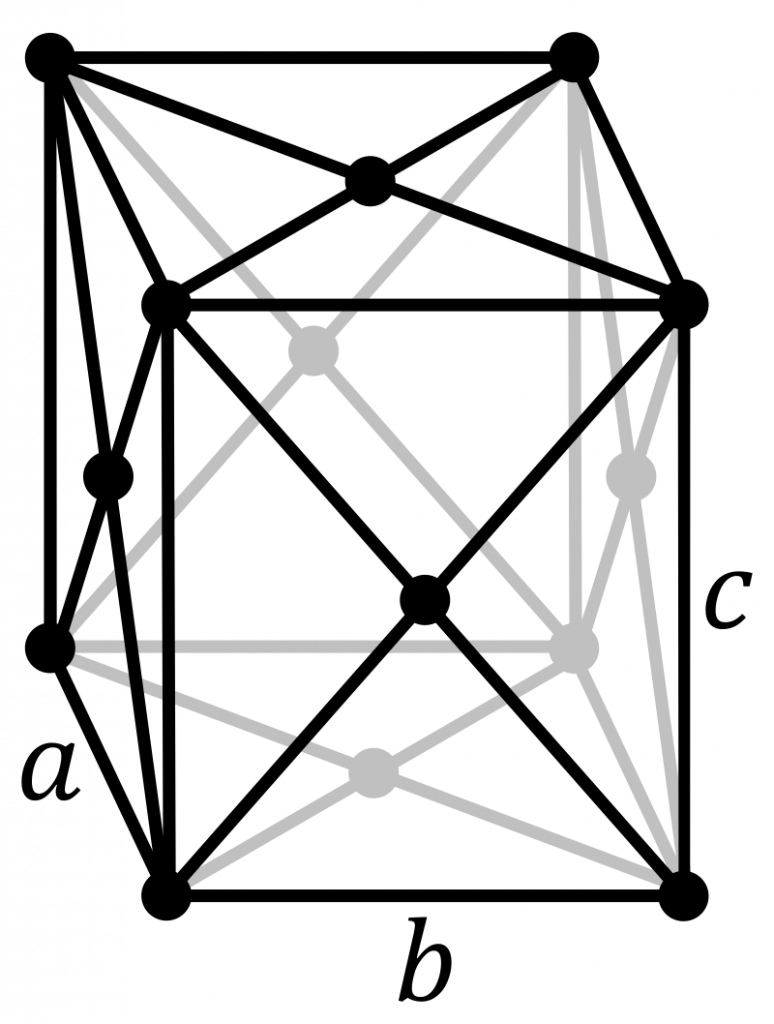
The conventional unit cells for each of these lattices have all angles equal to \(90^{\circ}\). Primitive cells of each of the centred lattices do exist, but deviate from the shape shown above. It is convention that the cuboid cells are used for simplicity. If you would like more practice identifying other unit cells, practice drawing these lattices out and finding one of the primitive cells that represents these lattices. Click the links for the typical primitive unit cells of the base-centred, body-centred and face-centred orthorhombic lattices.