Bravais Lattices – The Triclinic Lattice
The Bravais lattices refer to the 14 different arrangements of lattice points that can be used to form a periodic arrangement of points in three dimensions. It is best to consider a crystal as formed of lattice points and a motif. Lattice points are identical points in the lattice, with all experiencing exactly the same environment around them (if the lattice is infinitely big). If a motif of atoms is placed at each lattice point the resulting arrangement of atoms perfectly replicates the crystal. This can be shown comfortably in 2D (with thanks to Stefan Bringuier for the image).

Infinite lattices are the concept used throughout crystallography, though processing infinite crystals as they are is not possible. These lattices are thus reduced down to their unit cells. This can be seen in the image above as the square shown on the crystal structure. The unit cell, when repeated in space, replicates the lattice perfectly. This allows further simplification of the crystal structure to a motif and a unit cell of lattice points, rather than an infinite arrangement of lattice points.
The shape of the unit cell must tessellate without leaving gaps. All 14 Bravais lattices are thus parallelepipeds. Parallelepipeds can be thought of like a cuboid where each face is a parallelogram rather than a square. There is no requirement on the angles associated with the parallelograms on each face, so consider that these can sometimes look nothing like cubes at a first glance. It is easy to see how parallelepipeds must tessellate successfully when considering how parallelograms would tessellate in two dimensions. The image below shows the unit cell associated with the triclinic lattice. This is the ‘freest’ unit cell, with no requirements on its lengths or angles.
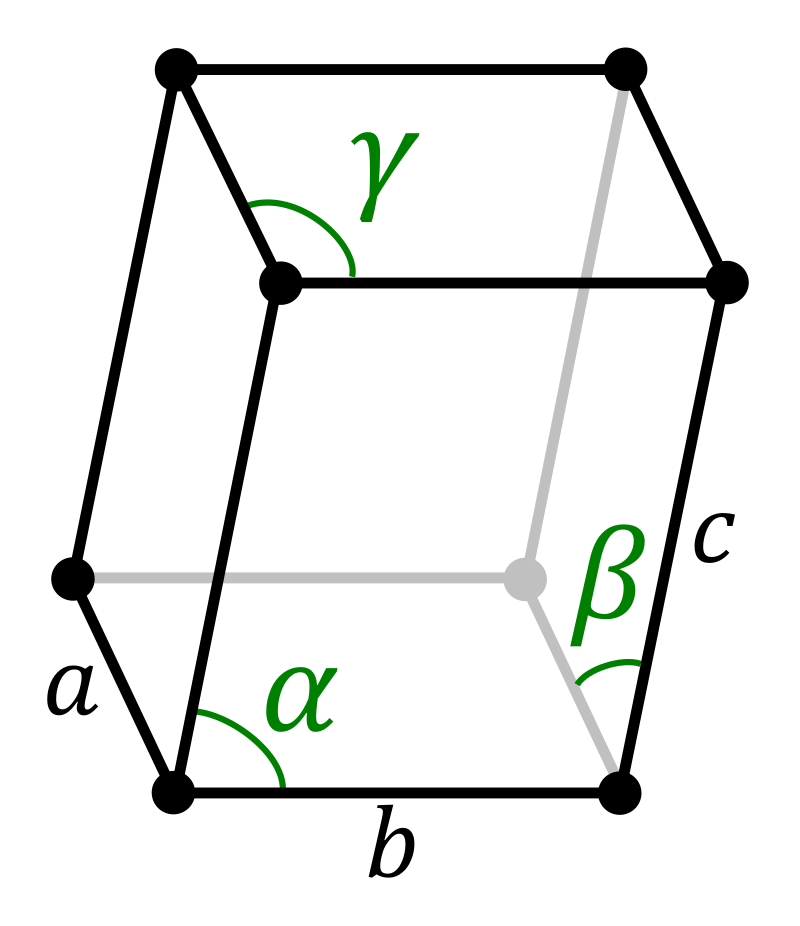
The triclinic lattice has no defined symmetry apart from the translational symmetry of the lattice points. a, b and c are used to represent the different unit cell vectors. Similarly, \(\alpha\), \(\beta\) and \(\gamma\) are used to represent the angles. The notation of the angles are best remembered as corresponding to the side not involved in determination of the angle. \(\alpha\) is the angle between b and c. \(\gamma\) is the angle between a and b.
The lattice points are represented as spheres at the vertices of the unit cell. When the unit cells are repeated in space, the vertices are connected. As such, only one lattice point is actually present in this unit cell. It is convention to represent this lattice point at the vertices of the unit cell. However, placing the single lattice point at the centre of the unit cell would produce an identical lattice when the unit cell is repeated.