Infinite Unit Cells
It is relatively straightforward to show that infinitely many primitive unit cells exist to represent a lattice. This is shown here for a hexagonal lattice.
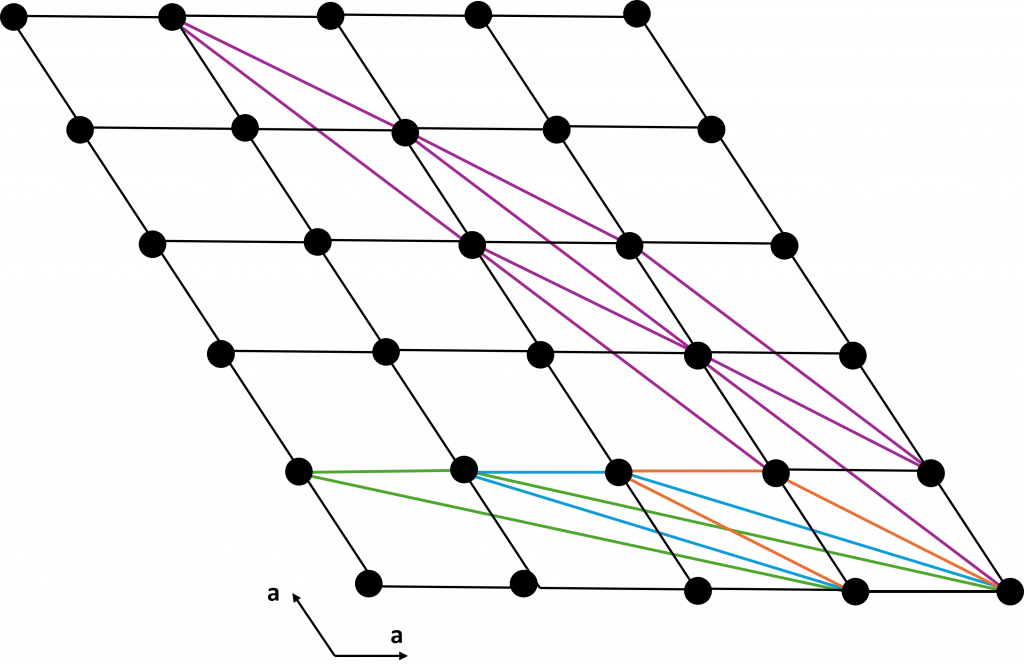
Each of the green, blue, orange and purple cells produces the hexagonal lattice when repeated, even if some of the unit cells look very distorted. To show that infinitely many unit cells exist, consider the orange, blue and green cells. From orange to blue to green, each cell represents a shifting of two of the lattice points by one of the unit cell vectors. This produces a new primitive unit cell. In short, without delving into mathematical proofs, the nature of the lattice means that we must be able to do this once and still have a primitive unit cell. The nature of the lattice also means we must be able to do it again (and again…).
This is shown here for the hexagonal lattice, but the simple idea behind the proof holds for all lattices. Every lattice has an infinite number of unit cells associated with it.