Primitive Unit Cell of Base-Centred Orthorhombic Lattice
Beginning derivation with a unit cell which has all angles equal to \(90^{\circ}\) simplifies the process significantly, allowing simple working in a 2D representation. A 2D representation of the lattice is shown below, from the perspective looking down the unique axis of the conventional base-centred unit cell.
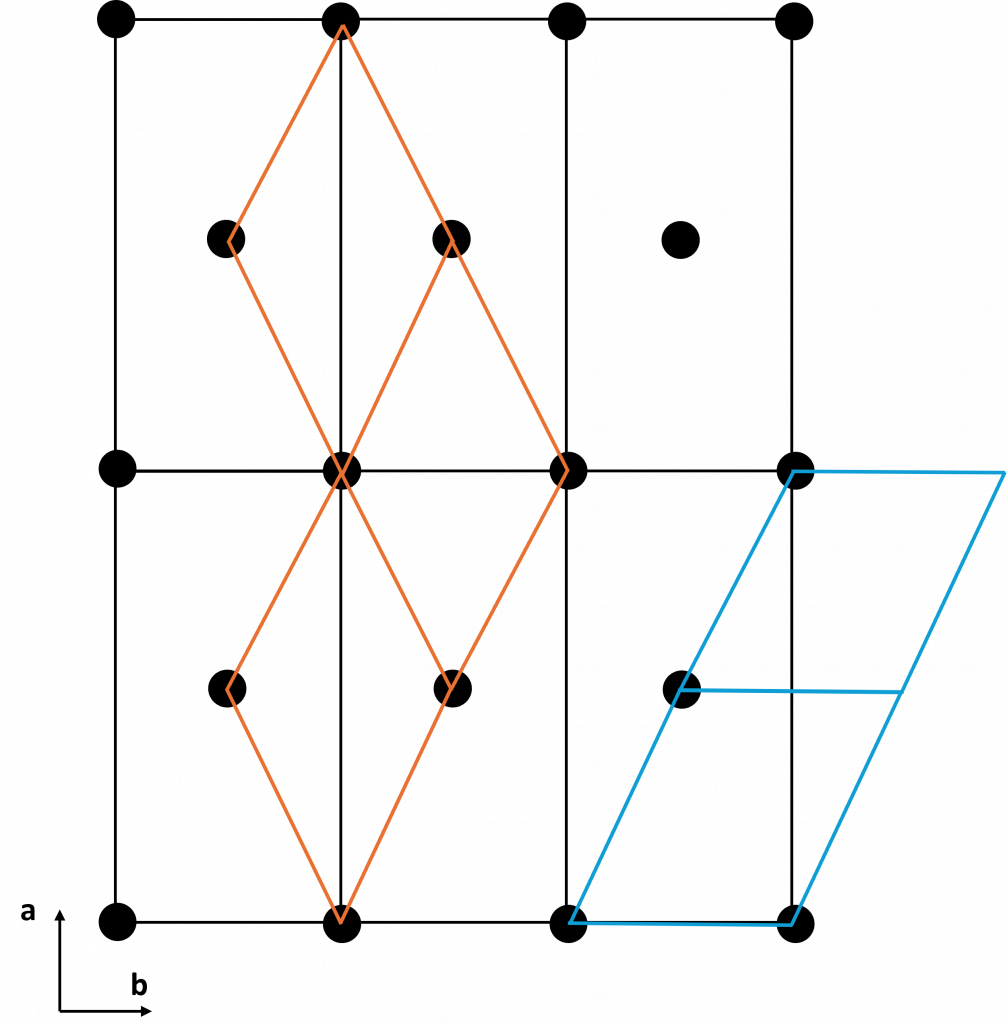
The cells above represent two of the primitive cells possible from a base-centred orthorhombic cell. These are the simplest primitive cells, though infinitely more are possible. Below is the 3D representation of the orange unit cell. The c axis remains unchanged in both cells.
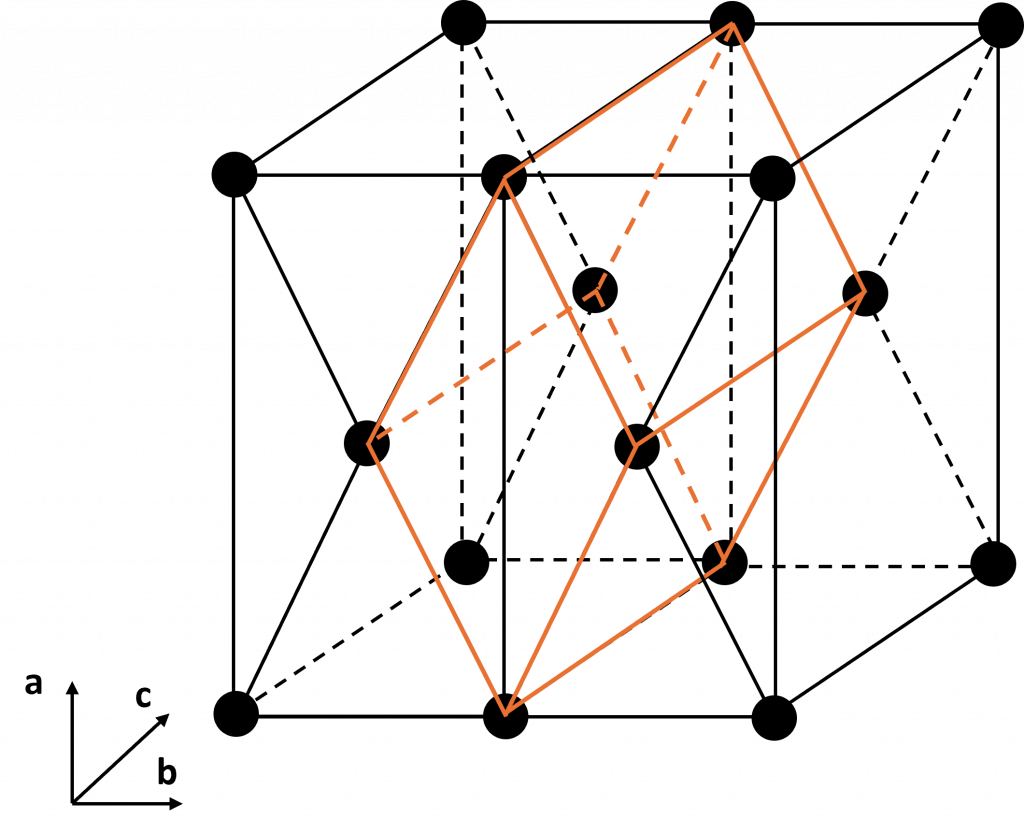
The new unit cell axes of the orange cell are determined like so: $$\mathbf{a’} = \frac{1}{2}\mathbf{a} + \frac{1}{2}\mathbf{b}$$ $$\mathbf{b’} = \frac{1}{2}\mathbf{a} – \frac{1}{2}\mathbf{b}$$ $$\mathbf{c’} = \mathbf{c}$$
The new unit cell axes of the blue cell are: $$\mathbf{a’} = \mathbf{a}$$ $$\mathbf{b’} = \frac{1}{2}\mathbf{a} + \frac{1}{2}\mathbf{b}$$ $$\mathbf{c’} = \mathbf{c}$$