What actually is diffraction?
Many people would think of Bragg’s Law. Bragg’s Law is correct. However, the explanations of it are often lacking. Explanations of Bragg’s Law often discuss reflection, and images showing reflection do not help this problem.
A full explanation of scattering and diffraction is given here, to be considered as the origin of Bragg’s Law.
Scattering
Scattering of photons considers the wave-like nature of light. Diffraction is often explained as an extension of the double slit experiment, in which scattering from the slits produces interference patterns.
Consider dropping a stone in a pond. Ripples are seen emanating in all directions. If two stones are dropped at identical times, the ripples from each individual stone can overlap and interfere, creating areas of greater displacement (constructive interference) or regions of lesser displacement (destructive interference). This is equivalent to the situation shown in the images below.

Each blue dot is a scatterer. In a diffraction experiment, a series of scatterers all scatter light in all directions (in 3D, though here we are examining it in 2D for simplicity). In the image above, the light originates from perpendicular to the screen (imagine shooting a beam of light from your eyes onto the page). If we extend this to an array of many scatterers, rather than up to 4, the below image is obtained. Note that the exact images obtained depend on the frequency of light used and the arrangement of scatterers.

This gives a much sharper pattern, with constructive interference occurring along only very specific directions.
Typical Diffraction
In a typical diffraction experiment the light does not arrive perpendicular to the measurement plane. Our analysis must be changed slightly to reflect how the scatterers interact.
In the above analysis, the starting phase of the wave emanating from each scatterer was identical, as the distance from the origin of the incident beam (your eyes) to each scatterer is (almost) identical.
If the beam comes in from a different direction, the distance travelled by the beam to reach each scatterer is different. The phase of the wave changes as it travels, so travelling a different distance to the scatterer gives it a different phase when it is scattered. As such, the starting phase of the wavefront emitted by each scatterer is different.
The below image shows the result of this. The blue line depicts the origin of the incident beam of light.
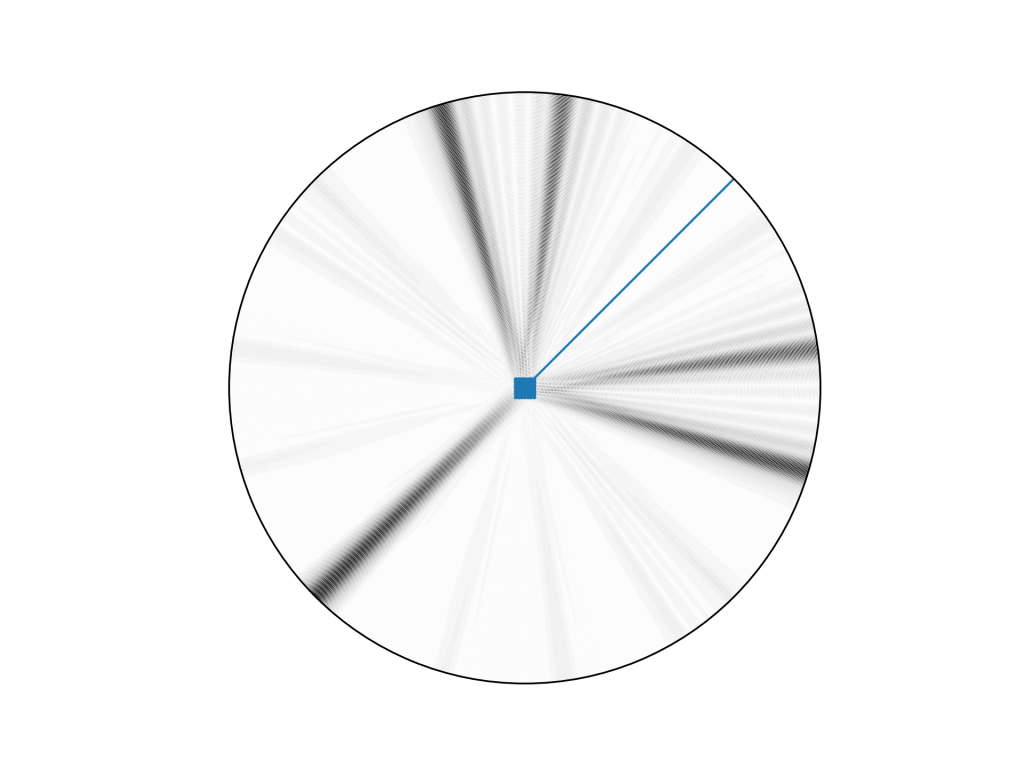
How is this a diffraction pattern?
The visualisation shown above is a calculation of the wavefront produced by scattering. Plotted on the edge of the below figure is the amplitude of the wavefront in each direction. The calculation of this from individual scattered waves is given in the python notebook provided at the end of this page.
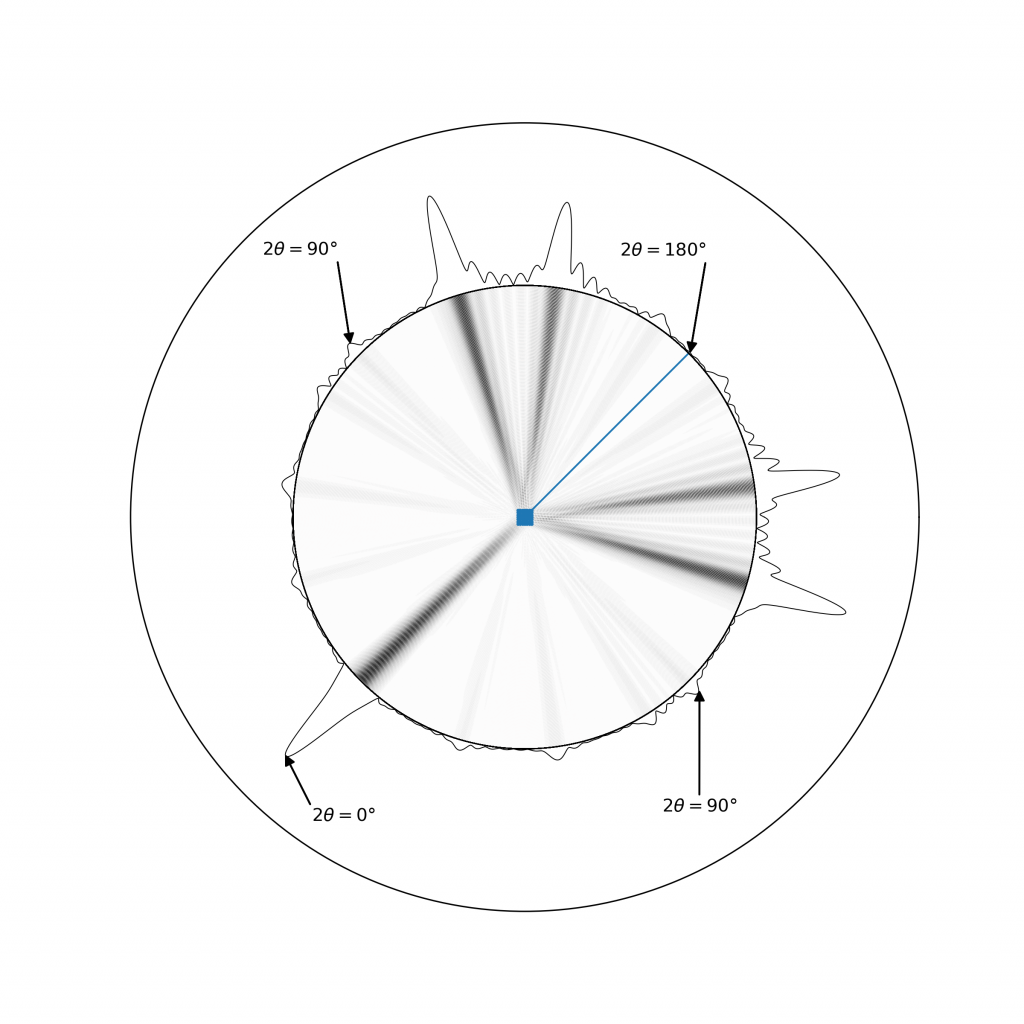
As you can see, we have the interference pattern as a function of \(2\theta\). In an experiment, the number of photons detected at each angle are what is measured. The detector in lab diffractometers simply moves in an arc around the sample holder. These photons, acting as particle-like when they are detected, follow a probability distribution proportional to the square of the amplitude of the wavefront (from quantum mechanics). If we combine this with unzipping the plot, we obtain the data plotted in the format usually seen.
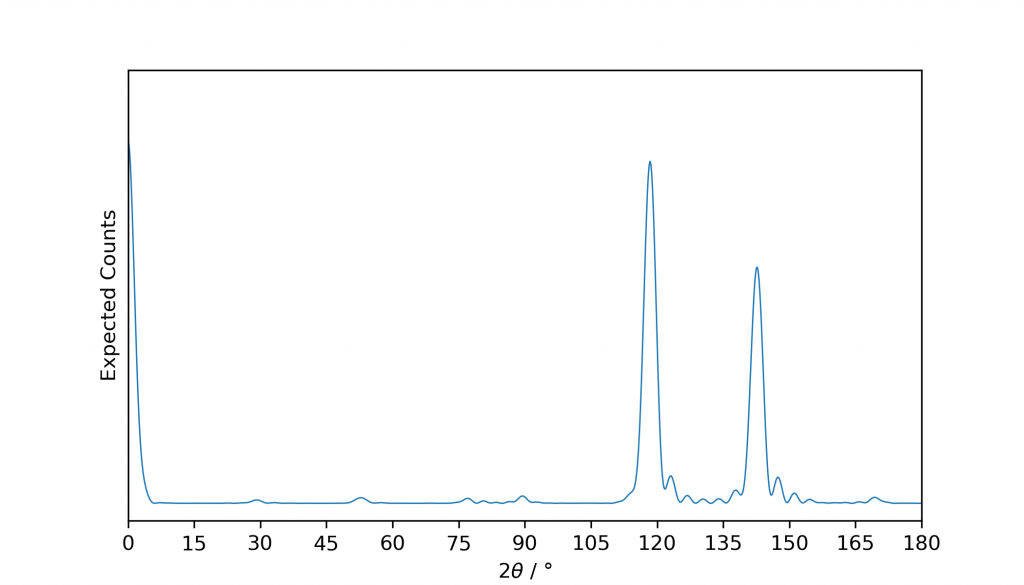
As mentioned previously, these are 2D visualisations in order to help understand how diffraction works. In the ‘many scatterers’ examples given, it is important to remember that scattering occurs in all directions in 3D space, and that a periodic crystal also repeats in all three dimensions. In the above, scattering has only been considered in two dimensions, with all scatterers and observed scattering occurring within a plane.
A python notebook is provided below, allowing you to fiddle with the generation of scattering patterns yourself. It also provides an explanation for how I calculated the expected photon count from the wavefronts.
The calculations are somewhat laborious, and as such this does not represent a truly infinite periodic crystal. It is intended that this page and notebook give you an idea of the concept of diffraction originating from scattering in all directions, rather than reflections as is often depicted.
Remember, diffraction is not due to reflection! It originates from the constructive and destructive interference of waves scattered in all directions.
Python Notebook
The python notebook is uploaded as a HTML file. You can simply have a look through the maths/explanations or download it and copy the code into a jupyter notebook to produce your own images! The code has been left fairly visible (i.e. not using classes or functions) so that those relatively new to Python can hopefully follow and edit as they wish.